线性

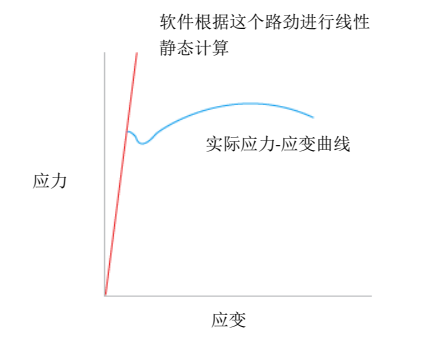
在Altair（HyperWorks）中，线性表示材料线性弹性行为。也就是说，应力-应变曲线的线性部分，一个直线按照胡克定律：σ=εE。这条直线方程就是 y=mx跟原点有交叉。曲线的斜率就是弹性模量，E，也是常数。在真实情况下，过了屈服应力，材料会按照非线性曲线走，可是求解器还是会按照线性曲线走。超过极限应力，部件应该破裂，可是线性静态分析不会显示失败。它只会显示没有破坏的部件，在失败位置显示有很高的应力。也可能会看到不现实的

大变形。工程师需要比较最大应力和屈服应力或者极限应力，然后决定部件是安全还是失败的。所以工程师必须考虑材料和载荷在线性静态情况是否可行。

 

 

 

静态

静态分析有两个条件：

1． 力是静态的，也就是说，力是常数，静负载

 

 

 

2． 平衡条件：∑ Force = 0, ∑ Moments = 0

∑Fx = 0 ∑Mx = 0

∑Fy = 0 ∑My = 0

∑Fz = 0 ∑Mz = 0

 

有限元模性在每个节点应该满足这个条件。在每个位置，外部力的总和应该等于反作用力总和。这是最常用的分析类型。所有航空，汽车，海洋和土木工程行业会用线性静态分析。

 

HyperMesh线性静态分析举例

 

理论结果

在机械学里，静态状况意思就是平衡力和扭矩（V=0）。静态载荷应该没有变化。要是载荷变化很慢，结构反应可能考虑用静态分析确定。但是载荷变化很快的话（相对于结构的反应能力）就需要用动态分析确定。计算静态问题，所有有限元分析求解器会算下面的方程：

Kx = f

l K: 整体刚度矩阵

l x: 需要确定反应的位移矢量

l f: 施加到结构的外力矢量

 

我们现在考虑一个简单的静态例子来帮助我们理解静态分析。例子如下：

 

 

 

这是二级柱，两个均等部分，有不一样的横截面面积。

下面说的办法可以扩展到任何问题。先需要用节点和单元建模结构。明显这个问题至少要两个单元，每一部分一个单元。

 

我们先从Altair（HyperWorks）中来考虑下面的有限元模型解决这个线性静态问题。在这个例子中，我们将使用杆单元，如下图片：

 

 

 

模型有三个节点（1，2和3）以及两个单元（1和2）。相关的材料横截面面积是A长度是L。假设每一个节点只有一个自由度（x）。这个一维杆单元的刚度矩阵是：

 

 

 

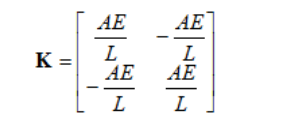
然后我们可以用输入数据计算每个单元的矩阵：

 

 

 

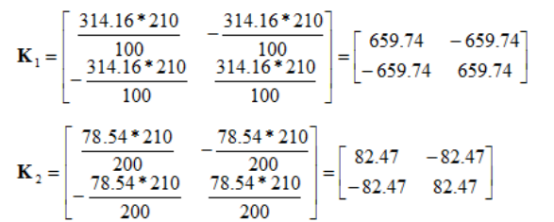
下一步要组合这两个单元刚度矩阵为整体刚度矩阵：

 

 

 

现在需要定义力和位移矩阵的向量：

 

 

 

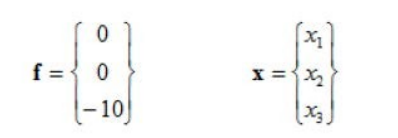
最后，整个系统可以用整体刚度矩阵，位移矩阵和力矩阵来代表：

 

 

 

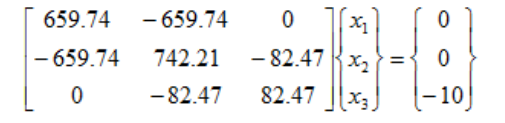
节点1是固定的，所以这个节点位移是零。因此我们可以消除第一行和第一列。

 

 

 

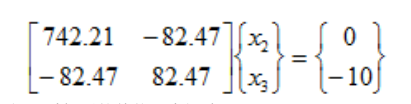
解决这个问题我们需要两侧同乘倒置的整体刚度矩阵。

 

 

 

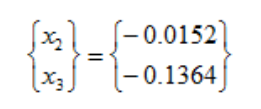
这就给出了节点2和3的位移值。确定位移矢量以后，就可以确定单元应变、应力和力。

 

应变

 

 

 

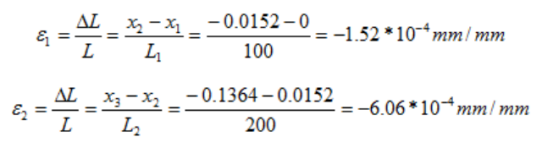
应力

 

 

 

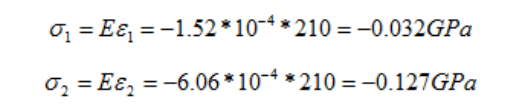
力

 

 

 

这是很简单的例子，可是精心总结了有限元分析在线性静态问题中的使用。以上所有的计算是求解器计算的。要是用户需要更详细的有限元分析信息，可以在网上文档或者参考书籍中找到。