什么是自由度？

 

 

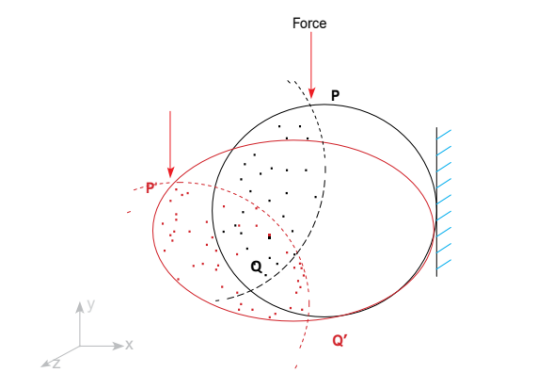
在上面所给出的例子中，一个对象被固定在一点，并在 P 点施加了一个力。由于受到外力，对象产生形变，P点也移到了P’点。

 

何时我们才能说我们知道上述问题的解决方案？

当且仅当我们能够完全定义每一个粒子的变形位置。

完全确定一个物体在空间位置所需要的参数（运动、坐标、温度等等）的最小数被称作自由度 (dof ) 。

思考下面的二维（平面）问题。假设已知起点在左下角。参照起点，如果要完全确定A点的位置需要两个参数，即x1和y1，也就是 2 个自由度（平移x和y）。

 

 

 

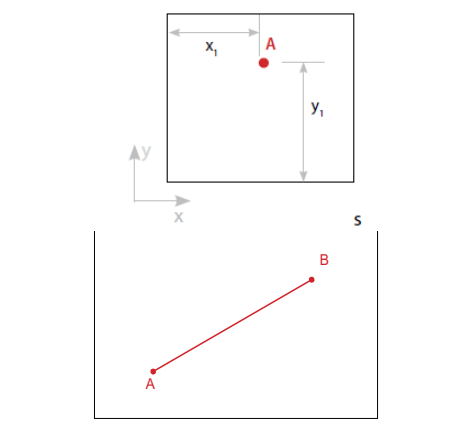
假设 A 点是线上一点，那么现在除了两个平移之外还需要定义一个角度，即 3 个自由度（两个平移和一个旋转）。

 

 

 

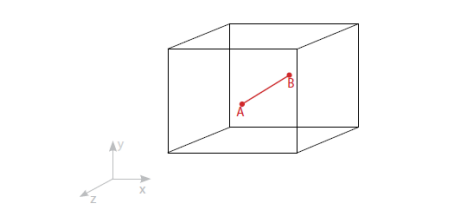
假设 A 点和 B 点被移出平面，这条线相对于三条轴自由旋转。完全确定 A 点的位置需要至少 6 个自由度 3个平移(Ux , Uy , Uz)和 3 个旋转(θx , θy , θz)}。

自由度是一个非常重要的概念。在有限元分析中用它来代替个体的计算点。一个给定的网格模型的自由度总数相当于节点数乘以每个节点中自由度的数量。

并不是所有单元的每个节点都有 6 个自由度。自由度的数量取决于单元的维度（一维、二维、三维）、种类（薄壳、平面应力、平面应变、膜壳等）以及分析类型。例如，在结构分析中，一个薄壳单元上的每个节点拥有 6 个自由度（位置未知，3 个平移和 3 个旋转），同样的单元在热分析时每个节点只有一个自由度（温度未知）。

 

对于一个初学者了来说可能有些复杂，实际上在给不同的单元类型分配特定数量的自由度背后包含着许多逻辑、工程以及数学思想。

 

为什么进行网格划分？什么是有限元法？

 

 

FEM

- 一种数值计算法

- 一个实际问题的数学体现

- 近似法

有限元法只在数量有限的点时进行计算，然后将结果插值于整个域（表面或体）。

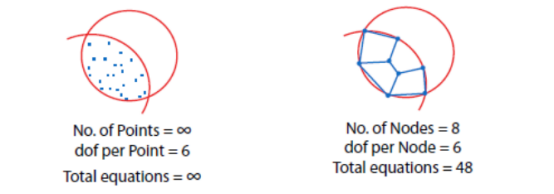
有限 – 任何一个连续的对象都有无限个自由度，在这种情况下是无法解决问题的。通过离散化和建立网格（节点和单元），有限元法把无限个降低到有限个自由度。

单元 – 所有的计算都在有限数量的点即节点进行。加入节点形成一个特定形状的实体，例如三角形或四边形，被称为单元。在任意计算点之间，会根据单元的形状运用插值函数获得一个变量的值（如位移）。

方法 – 所有的工程问题都可以用 3 种方法解决。有限元分析属于数值计算法。

 

如何从少数的计算点插值结果？

可以肯定的是有限元分析在有限数量的点进行计算，但问题是它如何在计算点之间计算未知点的值。

可以通过插值获得。请思考下图所示的一个 4 个节点的四边形单元。一个四边形单元可以使用下面这个线性插值公式：u = a0 + a1 x + a2 y + a3 xy

有限元分析计算外部节点 1，2，3，4 的值，即 a0, a1, a2, a3 是已知的。

 

 

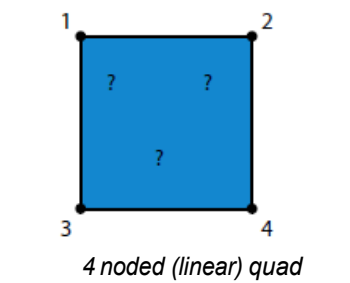
仅通过指定上述方程中 x 和 y 的坐标就能够轻易地确定任意两点变量的值。

对于一个八个节点的四边形，可以使用下方抛物线插值函数：

u = a0 + a1 x + a2 y + a3 xy + a4 x2 + a5 y2 + a6x2 y + a7 xy2

 

 

 

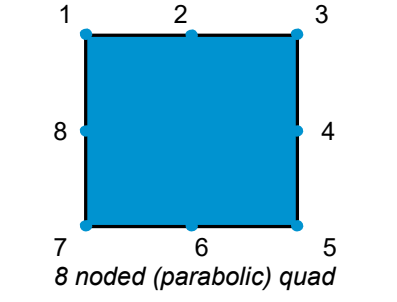
如果计算点（节点和元素）数量增加，精确度如何？

通常情况下，计算节点数量增加，精确度也会增加。

假设给你 3 条直线，要求你在一个圆内选出最合适的位置，并计算出三角形的面积然后与圆的面积进行比较。接着重复进行 4,6,8,16,32 和 64 条线这几种情况的比较。

 

 

 

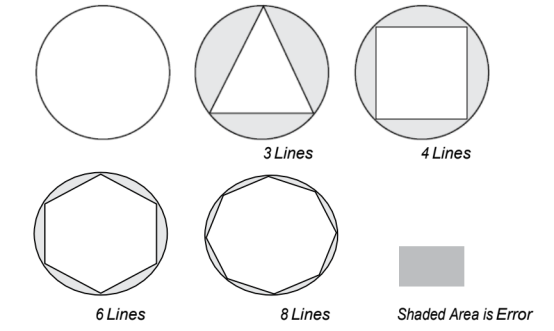
通过增加线条实现误差范围的减少。直线的数量可看作有限元分析中单元的数量。

此处圆的面积（π r2）确切值为 100。三角形的面积为 41，四边形的面积为 64，以此类推。答案 41 或 64不是全部适用，但是 80 或 90 则考虑了计算成本并体现了相应的设计理念。

 

 

 

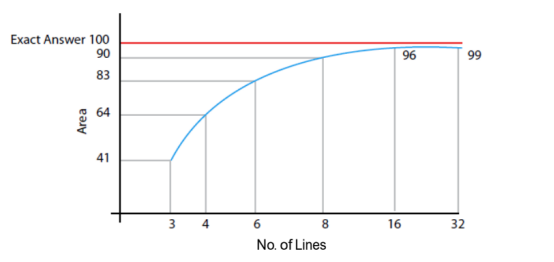
既然节点和单元的数量越多，精确度越高，那么为什么不使用最大量的节点和单元建立一个精细的网格？究其原因是解决方案的时间同(dof)n是成正比的，n可以是 1 到 4 之间任意一个数，这取决于分析和求解器的类型。同时，由于显卡内存限制，大规模的模型在计算机上难以处理。分析人员需结合现有硬件资源，在期望精确度和能够处理的单元尺寸(间接决定dof数量)之间获得平衡。

 

假设使用解析法花费一个月的时间得到非常接近 100 的结果，那么有限元分析运用合理的网格尺寸能够在一天之内得到 90 的计算结果。在工业上，快速的、符合逻辑且合理的解决方案远比绝对精确要重要。

 

有限元分析的优势

结果可视化：对于简单的几何形状，如简支梁或悬臂梁，很容易实现某点的最大应力和位移的可视化。但是在现实工程中，具有复杂几何形状的零部件或装配件都是由不同材料不连续的对象构成，多变的约束和复杂的载荷随着时间和作用点的变化而变化。并且会随着残余应力和连接处的焊接等变得更加复杂。正因为如此，很难预测故障位置。想象一下，如果有人给你一个复杂的发动机缸体，要求你根据已给的受力情况预测故障的位置。除非你在相关领域有丰富的经验，否则很难成功预测出。但是借助 CAD 和 CAE 这样的工具，以适当的方式建模，就能很容易获得应力等高线图，清晰地看到高应力区域和位移的大小。

 

以前，零部件都是由经历很多测试和失效形式的经验丰富的工程师进行设计。现在，在大多数机构中，设计工程师都很年轻，他们使用像 CAD/CAM/CAE 这类的工具，能够帮助他们提升自信。