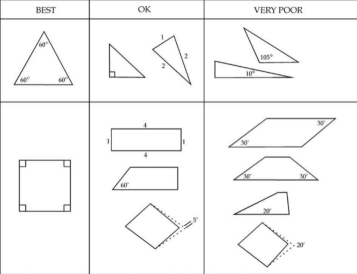
单元质量是一个经常谈论但从来没有真正理解的话题。原因很复杂，但是和单元质量的相对性，定义方法的近似性这两个方面有关。有限元法中每种单元类型有一个局部的参数坐标系，物理坐标系（无论是单元坐标系还是全局坐标系）和参数坐标系的匹配程度就表示了单元质量的好坏。下面是一些单元质量的图形表示。你最好遵循这些指标，但是有时过于拘泥地要求每个单元都在可接受的指标之内需要付出过多的努力，也是不值得的。
在这种情况下你需要自己做出判断。划分网格时总是对网格做一个快速检查，问一问身边的专家对于特定的有限元程序的特定单元应该指定什么样的质量指标值。要注意到，在这些情况下“正确”答案可能与下表中描述的相差很远，下表中“好” 和“很差”之间的范围是很宽的。
实体单元使用雅可比矩阵行列式与其理想值相比。
下面是一些常用的单元质量指标：
偏斜度
三角形的偏斜度(skew)通过计算寻找每一个点到对边中点与两条边的中点连线的夹角中的最小值得到。90 度减去找到的最小角就是三角形的偏斜度。
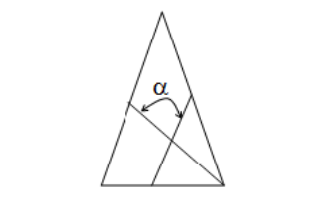
三角形偏斜度= 90 - α
四边形偏斜度通过单元两条中线的最小夹角计算。90 度减去找到的最小角四边形的偏斜度。
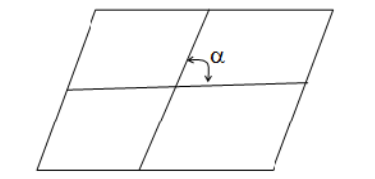
四边形偏斜度= 90 - a
偏斜度检查再 3D 单元的每一个表面上进行。
长宽比
2D 单元的长宽比通过单元的最长边除以最短边计算。3D 单元的长宽比检查在 3D 单元的每一个表面上进行。
翘曲度
2D 单元的翘曲度通过将四边形切分为两个三角形并计算两个三角形平面夹角得到。然后沿着另一组对角再切分一次就可以得到另一个三角形平面夹角。这两个角中的较大值就是 2D 单元的翘曲度。
3D 单元的翘曲度检查在 3D 单元的每一个表面上进行。
雅可比
雅可比率是给定单元偏离理想单元形状的一个度量。
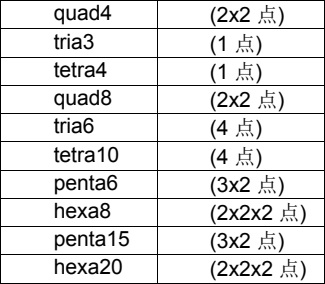
雅可比率的范围是-1.0 到 1.0，1.0 代表理想单元形状。理想单元形状和单元类型有关。测量方法是将参数坐标下的理想单元映射到全局坐标下的实际形状。例如：理想四边形在参数坐标系下的角点坐标为(-1,- 1)，(1,-1)，(1,1)和(-1,1)。
雅可比行列式关系到将局部参数空间的拉伸向全局坐标空间的映射。HyperMesh 在单元的每一个积分点（也叫高斯点）计算雅可比矩阵的行列式，并报告最小和最大行列式的比值。
不同的求解器使用不同的积分点模式，同一个求解器也可能在同一单元形状的不同单元使用不同的模式。如下是其中一种方法：
如果在所有高斯积分点都具有相同的局部拉伸，则雅可比为 1.0. 单元受到扭曲后雅可比值向 0 移动。雅可比小于 0 的单元是凹单元，大部分求解器不允许这种单元。该检查包含 1 阶和 2 阶单元，一阶三角形和四面体单元的雅可比总是 1.0。
