在学习Altair（Hyperworks）时，成功地完成有限元分析，需要正确理解各类单元的力学性能。在定义载荷和边界条件时,至少需要对各类单元的性能有基本的了解，而对单元形函数方面深层次的理论知识并不是必要的。

进行一个单元的有限元分析是研究单元力学性能的基本方法。求解结果可与理论解进行详细对比。该方法对理解不同求解器的单元定义方式有很大帮助。

下图描述了单一单元模型，各个模型对应着不同的载荷和边界条件。增加边界条件可对单元的力学性能作更深入的研究。

对单元来说，自由度是一个很重要参数，因为它们不但描述了给定条件下的单元的性能，而且反映了单元之间的兼容性。关于单元兼容性相关的内容将在我们将在下面章节中进一步讨论。

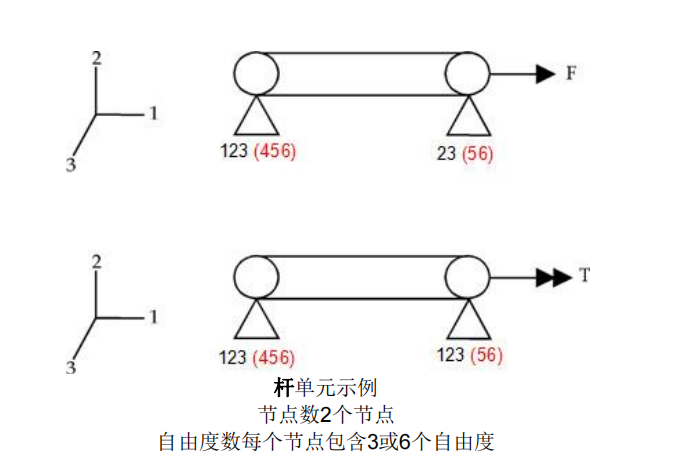
杆单元（Rod）

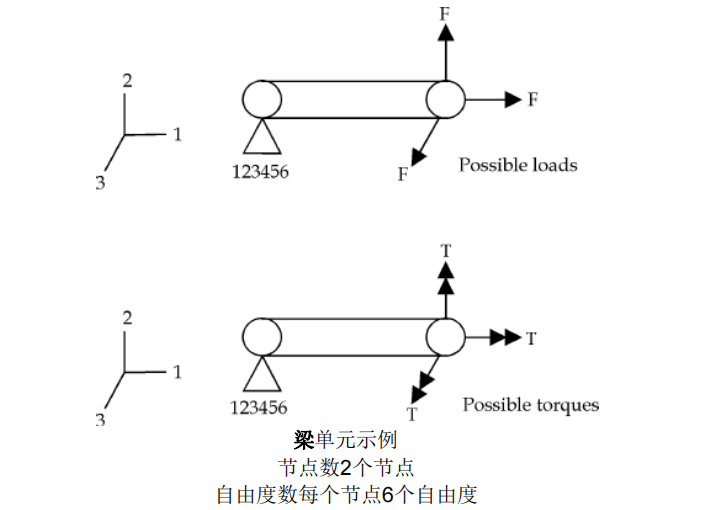
梁单元（Beam）

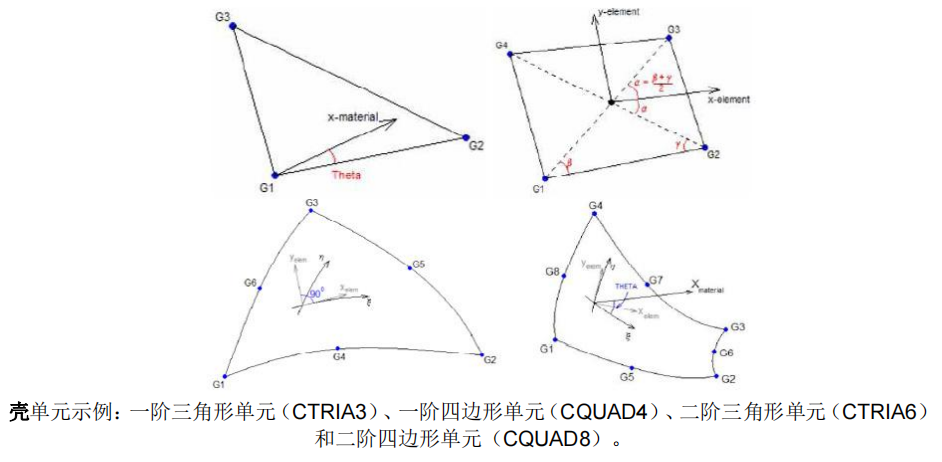
壳单元（Shell）

一阶壳单元有3或4个节点

二阶壳单元有6或8个节点

每个节点上有6个自由度

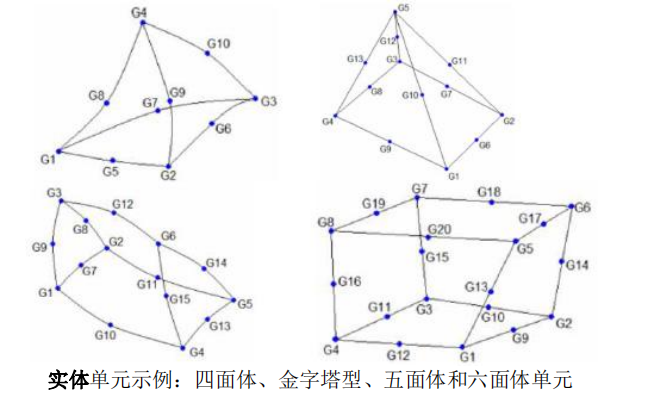
实体单元（Solid）

一阶实体单元有4、5、6或8个节点

二阶实体单元有8、12、15或20个节点

每个节点上有3个自由度

高阶单元

在学习Altair（Hyperworks）时，高阶单元指具有一个(或多个)中间节点的单元或基于几何的单元(如p型单元)，这类单元易于建模且精度较高。p型单元可通过增加基底函数的阶次来提高有限元解的精度，但其构成形式较为复杂，难于理解。

高阶单元的使用会引起一些复杂的问题。例如，当压力加载到壳单元上时，分布在各节点上载荷的和值应保持相同（F=P*A），4节点和8节点壳单元节点载荷分布如图所示。

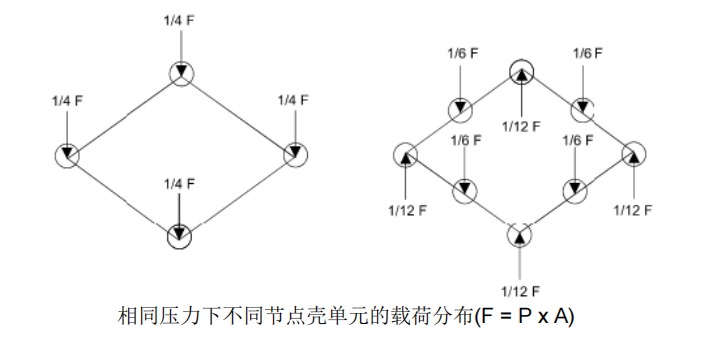
绝大多数软件能够处理这类问题，但用户需要理解此类问题的原因以及高阶单元的其他性质以避免错误 的应用。高阶单元通常使用三维实体单元模拟，因为这样可以大幅降低建模的时间以及网格规模。需要注意的是，求解时间并不会降低，因为模型的整体刚度矩阵取决于节点自由度数而非单元数量。

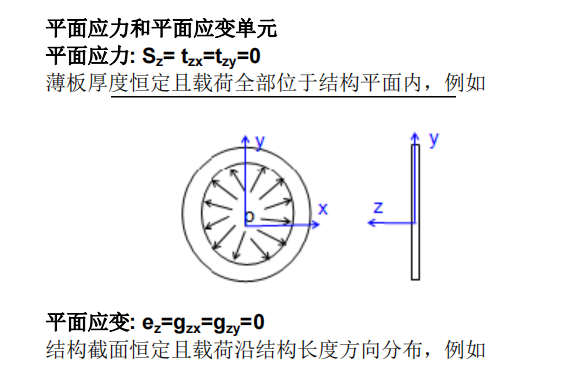
如若您对仿真软件有兴趣，或需要了解关于仿真软件的更多最新信息，可随时与我们联系，也可通过人工客服向我们获取更多仿真软件信息。