在Altair（Hyperworks）中，当结构的3个维度尺寸在同一量级时应该使用3-D单元。

3-D单元的适用场合

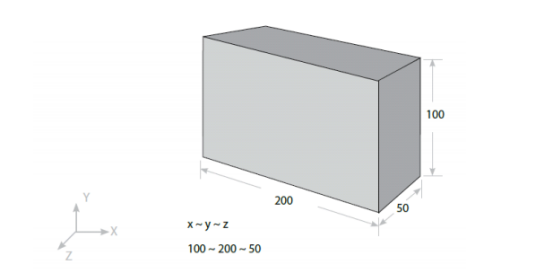
单元形状：四面体、楔形、六面体、金字塔

用户需要输入的数据：无

单元类型：实体

实际应用：齿轮箱、发动机体、曲轴等

3-D单元类型：

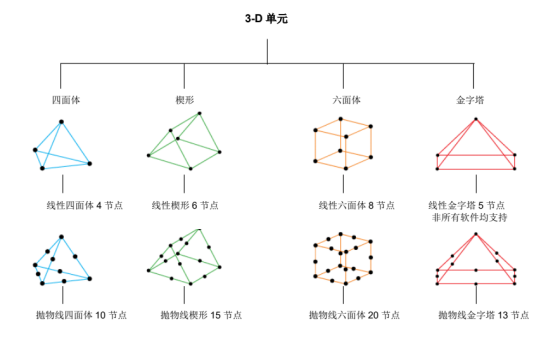
实体单元的自由度

在Altair（Hyperworks）中，2-D薄壳和1-D梁单元都支持6个自由度，但所有实体单元都只有3个平动自由度（无转动自由度）。例如一个10节点四面体单元总共有10 x 3 = 30个自由度。

为什么实体单元只有3个平动自由度而无转动自由度（物理解释）？

考虑一张纸片（2-D几何）或者一把长的铁尺（1-D几何）。他们容易被弯曲和扭转（转动自由度）。但是如果是除尘刷或者压纸之类的实体。他们通常不会承受很大的弯曲或扭转。因此，实体单元只有3个平动自由度而无转动自由度。

四面体网格划分技术

在Altair（Hyperworks）中，有两种四面体网格划分方法。

1）自动划分：这种方法局限于简单几何，并且要求CAD模型没有错误。用户只需要选择实体，软件会自动根据单元长度、质量指标进行划分。

优点：很快很简单。

缺点：生成的单元和节点数量很多。无法进行网格流向和网格模式控制（例如：螺栓、点焊、接触面模拟）。

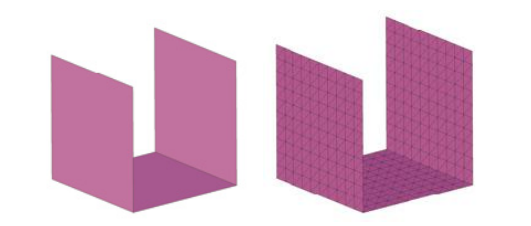
2）2-D（三角形）到3-D（四面体）：这是最常用的方法。在表面几何曲面上进行四边形和三角形网格划分。在四面体网格划分时四边形被自动切割为三角形作为四面体单元的基础。

2-D（三角形）到3-D（四面体）网格划分的步骤：

第一步：研究几何。

第二步：分割（孤立）曲面以便进行任务分配（如果有时间限制的话）。

a. CAE工程师1

第三步：合并网格

第四步：检查三角形单元质量（最小三角形角度大于15度，最大三角形角度小于120度，雅可比大于0.6），没有自由边，没有T型连接。

第五步：将三角形转换成四面体。

第六步：进行四面体单元质量检查（tet collapse > 0.1，雅可比和扭曲度(Jacobian, distortion)大于0.5，拉伸度大于0.2等）。如果必要，修整单元质量。

第七步：进行无约束分析或在假定约束下进行线性分析。

从三角形生成四面体的常见算法：

1)波前法：该算法很强大，是最常用的算法

2)Delaunay算法

3)三角形-四边形算法

所有算法都为三角形到四面体的转换提供两个选项：

1) 浮动三角形：用户在外表面生成的原始三角形和软件最终生成的四面体可以不匹配。选择该算法允许软件改变三角形单元分布（如果四面体网格生成过程出现一些问题）。该选项可以用于普通零件和区域的网格划分（没有高应力的区域，仅为提供刚度和质量的零件等）。

2)固定三角形：原始三角形和四面体网格的模式匹配。该算法可以用于希望进行网格合并/粘接的部位。否则会出现部件之间网格的不匹配（例如：网格连接不正确）。