有限元分析的类型（二）

动力学分析

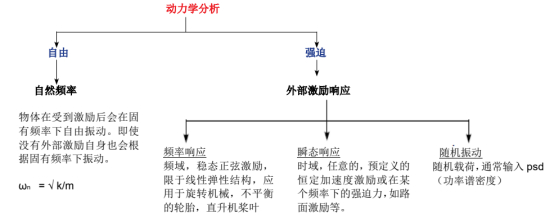
在线性静态分析中，求解的方程为 F = K * u。而动力学分析是基于另外的方程式：

[M] x¨ + [C] x˙ + [K] x = F(t)

x¨ = d2x /dt2 =加速度, x˙ = dx /dt =速度, x =位移

[M] x¨ = 0, [C] x˙ = 0, [K] and F(t) = 常值 - 线性静态分析

[M] x¨ = 0, [C] x˙ = 0, [K]是{u}的函数, F(t) =常值 - 非线性准静态分析

F(t) = 0, [C] x˙ = 0 and [M], [K] =常值 - 自由振动

以上术语都会用到 - 强迫振动

实际应用：自然频率是部件的基本设计属性。而强迫振动适用于部件受到随时间或频率变化的力，位移，速度或加速度激励

线性屈曲分析

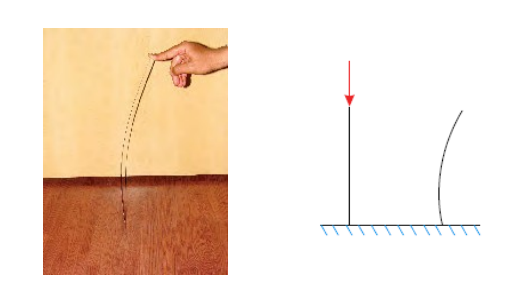
一些关键方面：

l 适用于只有压缩负载

l 纤细的梁和钣金件

l 弯曲刚度<<<轴向刚度

l 大侧向变形

软件计算输出结果：负载的临界值。

实际应用：土木工程中常用。机械工程中应用在真空容器，长变速杆分析等。

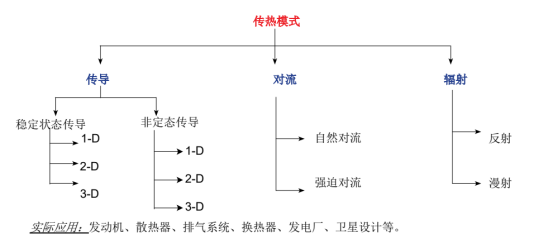
热分析

疲劳分析

材料学中，当循环荷载作用在材料时，疲劳是在逐步的结构损伤中发生的。名义最大应力值往往小于最大抗拉应力，甚至低于材料的屈服应力。疲劳发生在载荷反复加载和卸载作用在材料时。如果载荷超过特定阈值，表面微观裂缝会开始形成。最终的裂缝将达到一个临界尺寸，结构会突然断裂。结构的形状可以明显影响疲劳寿命；方孔或尖角会导致局部应力升高，形成疲劳裂纹开始的地方。因此，圆角、圆孔和平稳过渡的机构对结构疲劳强度的增加非常重要。

高周疲劳

历史上，大多数注意的情况，是超过 104 个周期而损坏的故障，疲劳区域应力较低，且变形是弹性的。

s-n 曲线

高周疲劳情况下，材料的性能通常由 s-n 曲线来描述，也称为 Wöhler 曲线。

这个简化的图形，纵坐标为循环应力，横坐标为疲劳寿命。

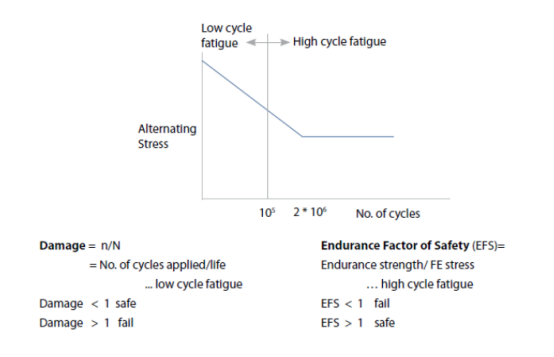
低周疲劳

应力足够高到塑性变形发生的地方，应力的作用就不是那么有用了，应变为疲劳提供了简单的解释。低周疲劳通常用 Coffin-Manson 关系来描述。进行静态分析和动力学分析并不能知道部件在一个循环载荷下的寿命。何况还要考虑诸如抛光、热处理、合金元素、脱碳和弧焊缝等因素。

实际应用：适用于组件受到动态载荷的情况，例如所有的汽车零部件。疲劳在现实世界的失效中占 90%。

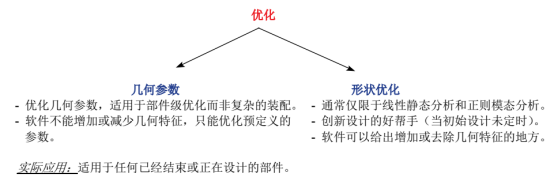
优化

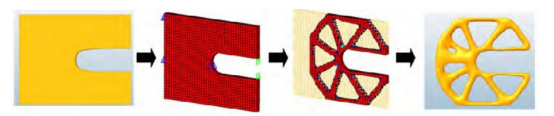
优化是Altair HyperWorks的整体优势之一。你可能需要区分优化方法对其在设计阶段中的位置，比如拓扑优化、形貌优化和自由尺寸优化用在概念设计中，尺寸和形状优化用在局部调整优化中。另外，通过区分设计变量，比如系统的变量在优化中是如何变化的，也可以区分优化方法。例如，拓扑优化的设计变量是单元密度，在尺寸优化中却是钣金件的厚度。