HyperWorks进阶教程：OptiStruct结构动力学基础（自动振动）

结构动力学指的是研究结构在动态载荷作用下的响应。常见的动力学响应包括位移、建度、加度、应力应交等。在工程应用中，可通过研究结构响应的模态或頻率响应等特性、确定结构的采展力成动力学性能。结构动力学可分为线性和非线性两大类。采用线假定的结构动力学分析，前满足大多数工程应用需求。非线性结构动力学问题涉及的影响因素很多，本书不进行介绍。

线性结构动力学最主要的应用是结构振动，按照振动过程中是否受到外激励的作用可分为自由号动和强造振动、按照分析对象的自由度不同，又可分为单自由度、多自由度或连续系统。工程中许(问题都可以简化为单自由度系统振动问题，研究单自由度系统的振动对解决工程问题有着实际意。而对于多自由度系统，则可以转换至模态坐标，这样便具有与单自由度系统类似的动态特性。

本章闸述结构动力学的基础理论，并引出结构振动的一些概念和要素。具体包括:自由振动和强迫振动的概念与特性;振动的时域及频域分析方法;固有频率及共振概念;阻尼及振动幅值的兴系;结构边界条件的影响等。

4.1 自由振动

振动即结构在平衡位置附近的往复运动，而自由振动指的是运动过程中不受外力作用，这种运动通常是由某些因素，如冲击激励，导致结构在初始时刻即已偏离平衡位置，而后遵循基本的动六学方程发生运动。

自由振动响应通常是一条随时间逐步衰减的曲线，对应的是OptiStruct中的瞬态响应分析类型包括直接法瞬态分析 DTRAN、模态法瞬态分析 MTRAN。

4.1.1 无阻尼系统

弹簧振子模型是一个典型的无阻尼单自由度振动系统，如图4-1所示，质量为m，弹簧刚度为k，无阻尼作用。质量块m在平衡位置附近发生微小偏移u(t)时，运动方程为

mi(t)+ku(t)=f(t)

当自由振动不受外激励作用时，/t)=0，此时方程的解为

"sin(w t)+u cos(w t)u(t)=-0

式中，“。与ǔ。为系统初始时刻的位移和速度;“。=、一，称为系统的固有(圆)频率或自然频率，下标n表示“naure”，单位为rad/s;振动位移u()为两个右端项的线性组合，分别为初始速度ǔ。引起的自由响应项“°sin(w-)和初始位移“。引起的自由响应项ucos(w-t)。

无阻尼自由振动如图4-2所示，它是一条无衰减的往复运动曲线，最显著的特征是振动的频率ω,不随时间发生变化，是系统的固有特性，取决于结构的刚度k和质量m。单自由度系统的固有频率只有一个ω,，而多自由度振动系统的固有频率则为|,,“,,“,,…，有若干个与自由度数相等的固有频率。

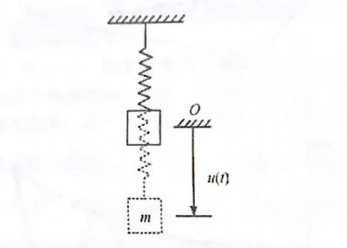
图4-1 单自由度弹簧振子

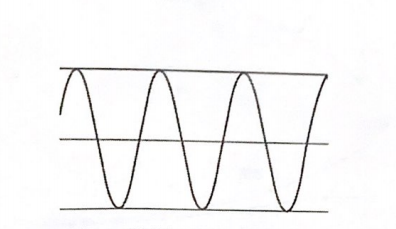
图4-2 弹簧振子无阻尼自由振动

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。