CMS是应用最广泛的超单元形式。在CMS算法中，OptiStruct通过计算子结构的低阶模态、剩余模态等，将子结构的运动表示为这些模态的组合。这些被选取的模态称为子结构的假设模态集也称为分支模态集或 Rilz基。理论上只要选取的假设模态集足够丰富，使用CMS 的分析结果就可以逼近原始的完整模型。
OptiStruct生成CMS的算法共分为五类：GUYAN、CBN、GM、CB、CC。其中，前三类用于OptiStruct结构静力学和动力学问题，后两类用于多体动力学求解所需的柔性体超单元。GUYAN 超单元仅可用于静力学问题分析，CBN及GM超单元既可用于静力学也可用于动力学。
10.2.1 GUYAN缩聚
静态缩聚也称GUYAN缩聚，是模态综合法在静力学工况中的特例，以对接刚度来表示子结构。用“,表示子结构不与外部连接的内部自由度,",表示子结构与剩余结构的对接(界面)自由度;」表示子结构内部自由度受到的外力作用,,表示在子结构对接自由度上受到的外力作用。
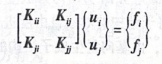
从式(10-1)的第一行可以得到
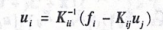
将式(10-2)代人式(10-1)的第二行，即可得到仅包含对接自由度“，的表达式：
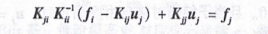
整理后得到
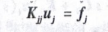
式中，K,为静态缩聚时子结构的刚度矩阵;,为静态缩聚时子结构的外力向量。
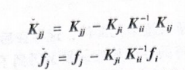
式(10-4)是静态缩聚的子结构表达式，子结构内部的静力被缩聚为一K„K了。进行静态统聚后、超单元中仅包含对接自由度“的对应项，内部自由度“被完全减缩。一般情况下，子结构的蒙接自由度数是远小于其所有自由度的，因此使用超单元将大幅缩减结构的自由度。需要说明的是、静态缩聚表达式(10-4)与完整计算式(10-1)的解是完全相同的，即静态缩聚是精确的，可以得到无误差的静力学求解结果。
静态缩聚还可以采用另一种表达形式，即以“作为子结构位移的主坐标。
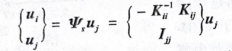
式中，内部自由度“:=-K'K“，它是式(10-1)在/=0时的解。可以证明式(10-5)等价于
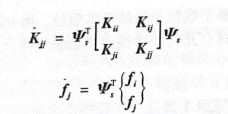
式中，亚为静态缩聚的基向量，也叫约束模态。它具有类似结构模态的特征:在模态法动力学分析中，结构位移用模态向量中和模态主坐标q表示。而在子结构静态缩聚算法中，子结构位移则以基向量业和对接自由度“来表示。
在OptiStruct中，静态缩聚使用CMSMETH卡片中的GUYAN算法执行，典型的静态缩聚求解文件设置如图 10-3所示，需要设置边界点集合ASET，CMSMETH卡片及T况引用。CMSMETH的方法设为GUYAN，可附加子结构外载荷 LOADSET 进行缩聚。
运行后将生成对接刚度矩阵K,和基向量业。矩阵K为jxj的方阵，基向量业共有个独立列向量。
在生成的.ou 文本中可查看超单元的矩阵规模，可使用 HyperView 查看.h3d 文件中的基向量业。
本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。
