Altair（HyperWorks）CAE软件基础教程【1D网格划分（1）】

何时使用1D单元

某一维度的尺寸相比另外两个维度大很多：

单元形状 – 线

用户提供的数据 – 剩下两个维度的尺寸，截面积

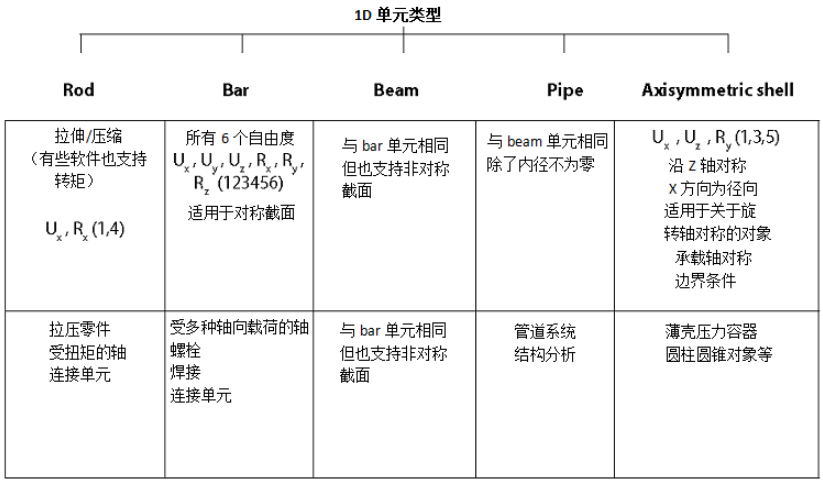
单元类型 – 二力杆、杆、梁、管、轴对称壳等

实际应用 – 长轴、梁、销连接、连接单元

刚度矩阵推导

什么是刚度以及为什么我们在FEA中需要它？

刚度‘K’定义为力/长度（单位N/mm）。物理意义 – 刚度等于产生单位位移所需要的力。刚度取决于几何形状以及材料属性。

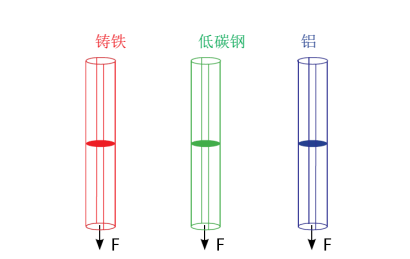
考虑3个几何尺寸完全相同的二力杆 – 铸铁、低碳钢和铝。如果我们测量产生1mm位移所需要的力，铸铁需要的力最大，然后依次是低碳钢和铝，即KCI > KMS > KAl。

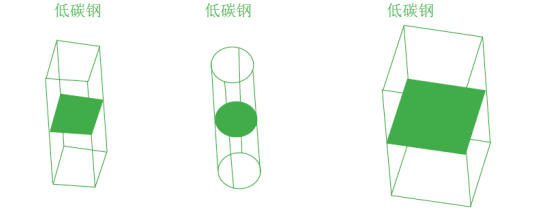
现在考虑3个相同材料不同截面的二力杆。同样，产生单位位移所需要的力是不同的。所以，刚度不仅依赖于材料，也依赖于几何形状。

刚度矩阵的重要性 - 对于结构分析，刚度是一个非常重要的属性。

线性静态分析的方程是[F] = [K] [D]。力通常是已知的，位移是未知的，而刚度是单元的特有属性。这就意味着如果我们用公式表达一个给定形状的刚度矩阵，比如线、四边形或者四面体，那我们就可以通过网格划分来表达任何几何形状并使用方程F = K D求解。

公式表达刚度矩阵的方法：

1) 直接法

2) 变分法

3) 加权残值法

直接法很容易理解，但是很难用电脑程序表达。而变分法和加权残值法很难理解，但是从编程的角度来说很简单。这就是为什么所有的软件要么使用变分法，要么使用加权残值法。

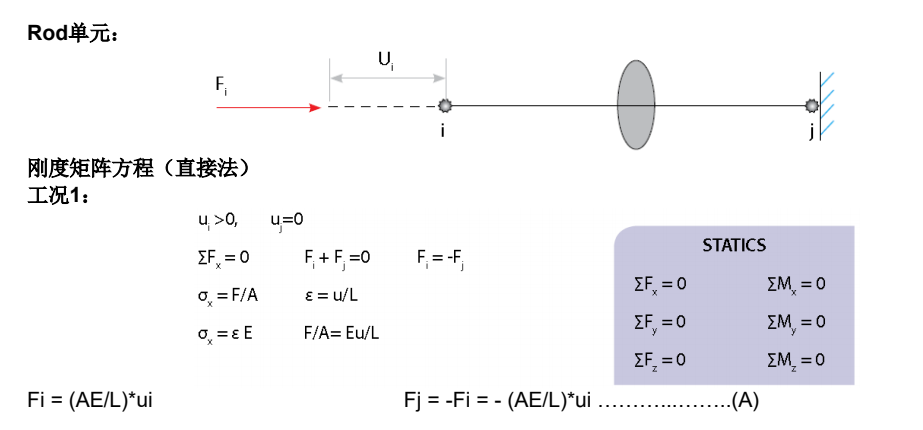
直接法推导二力杆单元的刚度矩阵：

直接法推导刚度矩阵的方法：

对于一个给定的单元，假设有n个自由度（比如，一个quad4单元的所有自由度 = 4*6 = 24）。

步骤1）假设第一个自由度 ≠ 0，并且其它所有自由度 = 0。生成方程1。

步骤2）假设第二个自由度 ≠ 0，并且其它所有自由度 = 0。生成方程2。

……

步骤n）假设第n个自由度 ≠ 0，并且其它所有自由度 = 0。生成方程n。

步骤n+1）所有方程相加，1 + 2 + 3 + 4 ………..+ n。

步骤n+1会给我们一个非常广义的刚度矩阵方程。

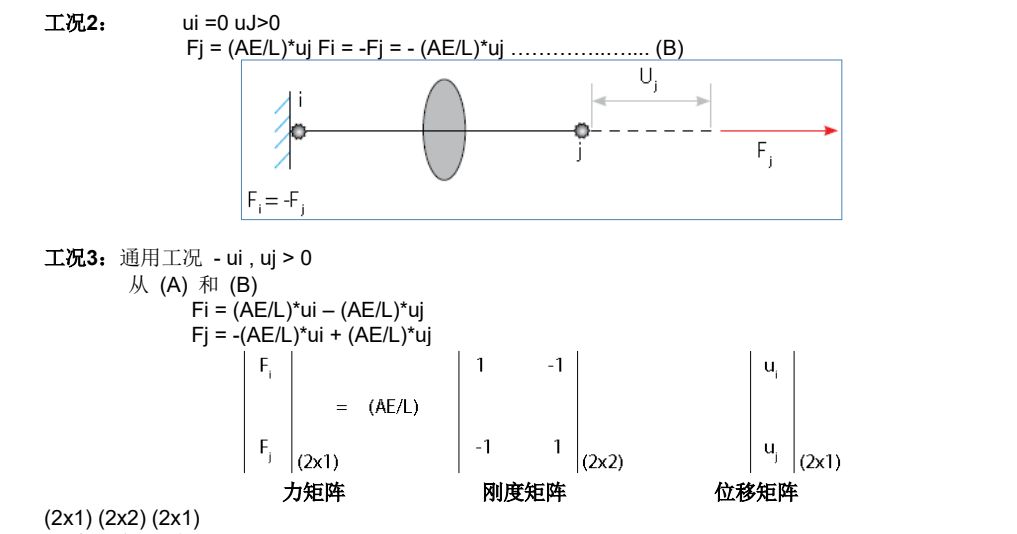
刚度矩阵的属性

l刚度矩阵的阶数与总自由度有关。

l一个奇异刚度矩阵表示结构未被约束并有刚体运动。

l刚度矩阵的各列是一个节点力的平衡集合，节点力产生对应自由度的位移。

l一个对称的刚度矩阵表示力与位移成正比。

l矩阵的对角线项全是正值表示一个力指向左边就不能产生向右的位移。只有结构在不稳定的情况下，对角线项才会是零或者负值。

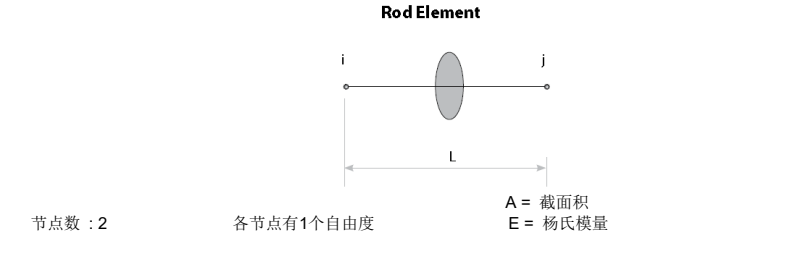
rod单元只支持拉伸或压缩，不支持剪力、弯矩和扭矩。在上述方程中，刚度矩阵的阶数是2x2，未知量的数量是2。

未知量的数量 = 自由度的数量 – 被“单点约束”约束了的自由度的数量（对于固定的节点，自由度记为0）

通常与模型中的总自由度相比，约束的数量是可以忽略不计的，所以未知量的数量近似等于总自由度。

刚度矩阵的阶数 = 总自由度 x 总自由度

对于一个给定的有限元模型，软件需要求解多少个方程呢？

假设模型中只有薄壳单元，共20,000节点（6 自由度/节点）。

总自由度 = 20000*6 = 120,000

刚度矩阵阶数 = 120,000x120,000

有限元软件会在内部求解的方程数 = 120,000

固体力学中变分法有限元与加权残值法有限元的等效表格

问题：在一个1D的rod单元的一端（自由端）施加一个集中拉力，另一端固定。

对应的微分方程和边界条件为：