HyperWorks进阶教程：OptiStruct强迫振动（简谐激励振动）

强迫振动指的是结构振动过程中受到外激励作用，即D)0。强迫振动的响应不仅与结构本身有关，还与外激励的形式密切相关。强迫振动通常依据外激励的形式可进一步细化为简谐激局动和一般激励振动。

简谐激励振动对应于OptiStruct的频率响应分析类型，包括直接法频率响应分析DFREQ和模法频率响应分析MFREQ。一般激励振动对应于OptiStruct的瞬态响应分析类型或频率响应分析这取决于采用激励的时域曲线还是频谱曲线。

4.2.1 简谐激励振动(时域)

简谐激励即正弦或余弦激励，/)=人sin(at)。通常把简谐激励下的结构振动分析称为稳态响应分析，此时结构振动的位移解为

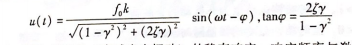
式(4-5)是忽略了初始条件(衰减自由振动)的稳态响应，响应频率与激励的频率相等,均为单一预率成分，而与结构固有频率无关。

y=“称为频率比，是简谐激励频率ω与结构固有频率ω,的比值;,k称为静力等效变形幅值√-v)+(25v)称为动力放大系数，响应u的幅值是在静力等效变形幅值,k的基础上叠加一个动力放大系数B。在稳态响应分析中，频率比y和动力放大系数B是十分重要的概念。随着频率比y的变化，动力放大系数B会发生很大的变化，如图4-4所示。

1)当y→0，即简谐激励远低于结构固有频率时B=1，振动幅值近似为人k。

2)当y→∞，即简谐激励远高于结构固有频率时B=0，振动幅值几乎为0。

3)当y=1，即简谐频率ω等于结构固有频率时，

称结构处于共振状态。此时，如果阻尼为零，那么共振振幅将无穷大。对于大多数实际结构，阻尼比0<<1此时动力放大系数B=7是一个有限数值。例如，阻尼比为0.01时，共振幅值是等效静力变形的50倍。

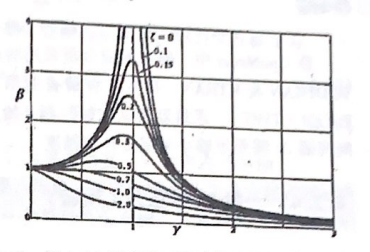
图4-4 频率比y及动力放大系数B

4.2.2 简谐激励振动(频域)

简谐激励振动是一种稳态的振动，通常在频域内进行分析。对微分动力学方程进行拉普拉斯变换，s=jw，在忽略初始条件后可以得到

ms`u(s)+csu(s)+hu(s)=f(s)

位移解u(s)在频域下有极为简洁的形式:

u(s)=-ms +e(s)+F(s)，“.=、-，y=“代入式(4-7)，写成频率比y以及阻尼比ζ的形式:将s=jw，5=-2√km

fy)u(y)=1-y+j(25y)k当等效静力变形“y)=1时，位移幅值‖(y)| 同为图 4-4 的形式。可求得式(4-7)分母 ms’+c+k=0时的共轭根s.，它们是单自由度振动系统的特征值5.. = -ζω„±jω ,ω =√1-w式中，ω 表示含黏性阻尼的结构振动频率，略小于ω.。小阻尼情形时，ω。≈ω.。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。