一般激励指的是任意表达形式的外激励，通常为非单频成分。例如，可以是多个不同频率的简谐激励叠加，也可以是连续不间断的随机载荷。
时域动力学分析中有两种分析方法。
1)使用“Duhamel(杜阿美尔)卷积”进行响应的求解。将任意激振力/(t)表示为无限多个瞬时力8(1-7)之和，然后通过积分方法叠加每个瞬时激励的自由响应，得到整个时段的响应。
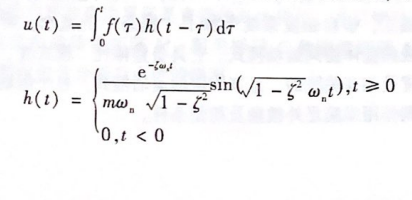
式中，h(t)称为脉冲响应雨数，是零时刻瞬态激励8(2)的位移响应；7为时间滞后量2)省接时域动力学方程进行等时间步长A:的离散化，通过还个时间步的依次求解得到动,学响应。
u(+ Δ)=F(u(),ù(),“())
在OptiStruct中，时域响应分析采用的是离散时间步的数值积分方法计算。对应于态分研列DTAN及NTRAN，具体过程请查阅第6章瞬态响应分析。用户只需要指定积分的寓股新NSTEP(TIME),求解器将从初始时刻开始，还一完成所有离散时问点的响应计算。一般来设。间间隔 A需要足够小来保证计算精度。
4.2.4 一般激励振动(频域)
如果外激励采用频域表达式八∞)，即时域表达式)的傅里叶变换，那么可以在频域上求解动力学响应，形式上为
u(w)-ma +jcw +h
特别的，外激励频谱/ω)=1时
h(ω)=u(ω)=-ma +jcw +h
式中，h(ω)称为单位频率响应函数，常用来评价结构在频域的基础响应特性。在OptiStruct中采用频率响应分析序列DFREQ或MFREQ完成计算。用户需要通过FREQi卡片来指定离散的频率列表，求解器将对每一个频率点计算响应曲线。
另外，OptiStruct中还支持采用逆傅里叶变换方法来获取时域响应。采用该算法时，首先计算频域响应u(ω)，而后通过逆傅里叶变换得到时域响应。求解序列为DTRAN或MTRAN，需同时定义时间步TSTEP(FOURIER)以及频率点FREQ。
本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。
