Optistruct黏弹性材料蠕动与松弛

有两类众所周知的材料：弹性固体和黏性流体。弹性固体具有确定的构形，在静载作用下发生的变形与时间无关，卸除外力后能完全恢复原状。黏性流体没有确定的形状，或决定于容器，外力在用下形变随时间面发展，产生不可逆的流动。实际上，塑料、橡胶、油漆、树脂、沥青、石油作肉、骨骼、血液等、同时具有弹性和黏性两种不同机理的形变，综合地体现了黏性流体和体两者的特性，材料的这种性质称为“黏弹性”

蠕变与松弛

黏弹性材料有两种应力、应变随时间变化的现象,

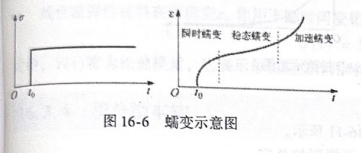
1）在恒定应力作用下，应变随时间而增加，这种现象称为“蠕变”。金属在高温下发生显著的蠕变现象，它可分为瞬时蠕变、稳态蠕变和加速蠕变三个阶段，如图16-6所示。在瞬时蠕变阶段、应变率随时间增加而减小;在稳态变阶段，应变率几乎为一常值;在加速蠕变阶段，应变率随时间迅速增加。

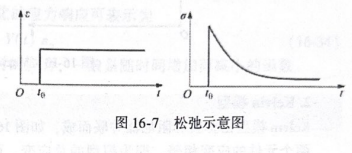
2）当应变恒定时，应力随时间而减小的现象称为“应力松弛”。它与蠕变现象相对应。图16-7表示一般应力松弛过程，开始时应力很快衰减，而后逐渐降低并趋于某一恒定值。工程中有的零件不允许应力松弛过快，高温管接头的连接螺钉就是其中的一个实例。

基本黏弹性模型

在线性黏弹性模型中，Maxwell模型及 Kelvin 模型是两个基本模型，复杂模型可以由这两个基本模型串联、并联或混联得到。下面简单介绍这两种基本模型的黏弹性特性。

1.Maxwell 模型

Maxwell 模型由弹性元件和黏性元件串联而成，如图16-8所示。设在应力σ作用下，弹性模量为E的弹簧和黏性系数为，的阻尼器的应变分别为弹性应变e和黏性应变s，串联元件中应力相等总应变为弹簧元件与黏性元件的和，可表示为

总应变率è为弹性应变率s和黏性应变率s.的和。

考虑蠕变情况，在恒定外力σ。作用下，应力率为0;考虑到瞬时弹性初始条件，可得到微分方程式(16-26)的解。

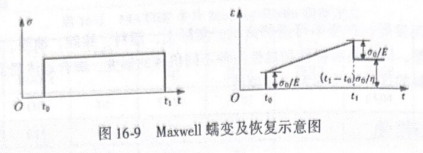
式(16-27)说明 Maxwel 模型有瞬时弹性，应变随时间线性增加，材料可以逐渐地无限产生变形，这是流体的特征。若在!=6时刻卸除外力，则原有σ。作用下的稳态流动终止，弹性变形部分立即消失，即有瞬时弹性恢复c。/E，残留在材料中的永久变形为(-6)0/n，如图16-9所示。

考虑应力松弛状况，施加恒定应变e。，则应变率为0;考虑初始时刻产生的应力为E。，可得

到应力解为

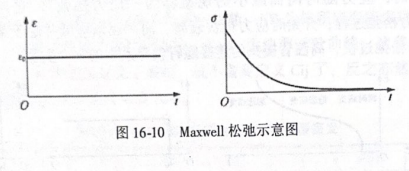
当保持应变。。时，应力不断减小，随着时间无限增加，应力衰减到0，如图16-10所示。式(16-28)中、7=E/7又称为延迟时间。黏度越小，松弛时间越短，即在较短的时间内衰减为0;黏麻越大，松弛时间越长，应力越不容易衰减为0。

2. Kelvin 模型

Kelvin 模型由弹簧和阻尼器并联而成，如图 16-11 所示。两个元件的应变相等，即为模型的总应变，而模型的总应力为两元件应力之和：

考虑蠕变情况，在恒定应力。作用下，微分方程式

可见应变随着时间的增加而增加，当1趋于无穷时，应变趋于σ。/E，像一弹性固体。但是Kel-vin 模型没有瞬时弹性，而是按照特定的变化规律发生形变：

逐渐地趋于应变的渐近值σ。/E。若在1=ㄣ时刻除去σ。，恢复过程的应变-时间关系为

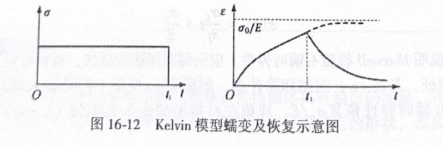
当1趋于无穷时，应变趋于0，体现弹性固体的特征，只不过是滞弹性恢复。Kelvin 模型的蠕变及恢复可用图 16-12 简单表示。

kdhin模型不表现应力松弛过程、因为阻尼器发生变形需要时间，要有应变率才有应力。所以当应变维持常量时、阻尼器不受力，全部应力由弹簧承受。

由上述可知：Maxwel模型能体现松弛现象，但不表示变，只有稳态流动;Kelvin模型可体我蟠变过程、却不能表示应力松弛。同时它们反映的松弛或蠕变过程都只是时间的一个指数雨数而大多数聚合物等材料的流变过程均较为缓慢，因此，为了更好地播述实际材料的黏性性质，常用更多的基本元件组合成其他模型。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。