Optistruct接触约束的引入

建立接触单元后，就需要将接触约束施加到接触单元上。接触约束的引人有两种方法，即罚函数法和拉格朗日乘子法。OptiStruct在默认情况下都是采用罚函数法。接触约束分为法向约束和切向约束。法向约束表现为接触物体法向不可侵人，在有限元分析中具体表现为法向接触刚度;切向约束表现为接触物体的切向摩擦滑移，在有限元分析中表现为切向接触刚度。

法向接触刚度

法向接触刚度的引人主要是为了满足接触面法向不可侵入条件，按其属性又可分为线性接触刚度和非线性接触刚度。

（1）线性接触刚度

接触单元在法向存在两种接触状态:一种为张开状态，即主从面之间没有产生接触:另一种为闭合状态，即主从面之间产生接触。理想情况下，在张开状态时，接触单元的刚度应该为零，接触状态时刚度为无穷大。但是在数值分析中，这样设置会导致数值振荡、结果不收敛。为了解决这个问题，会容忍一部分的精度损失，以保证结果的收敛，采取的策略是通过考虑主从面材料的刚度计算出一个相对较大的刚度作为闭合状态的刚度。为了避免在张开转闭合状态过程中刚度的突变往往并不将张开状态的接触刚度设为零，而是给一个相对很小的值，比如闭合接触状态刚度的1e-14倍，这样在损失很小精度的同时也保证了结果的收敛性。该过程也可以用图18-4简单示意，假定在初始时刻主从面之间存在U的间隙，此时主从面之间存在忽略不计的刚度K，在外力作用下，主从面之间发生相向运动，接触状态变为闭合，接触刚度变为K；在外力进一步的作用下主从面之间发生穿透，接触力增加，直至接触力与外力平衡，得到收敛解。在OptiStruct中，默认都是采用线性接触刚度。

（2）非线性接触刚度

在上述的线性接触刚度中，当接触状态由张开转为闭合时、接触刚度发生了突变，从刚度曲线上可以看到存在不光滑点，在少数应用中，这种突变会导致计算结果不收敛，而非线性接触刚度的引人可以很好地避免这个问题。OptiStruct提供了两种非线性接触刚度，分别为指数型和一次型，这两种接触刚度仅适用于面面接触。

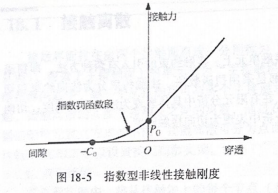
 图18-5 指数型非线性接触刚度

指数型接触刚度分为三段，其中，横轴表示接触问隙，纵轴为接触压力，用户需给出存在多大间隙(C)时即引入接触压力，在间隙为零时接触压力为多少(P)，这样就很光顺地过渡了张开、闭合接触状态改变导致的接触刚度的突变，如图18-5所示。指数型接触刚度可在PCONT卡片的STFEXP续行定义，其中的C、P。意义如上所述，OptiStruct对这两个字段还提供了 AUTO 选项软件可自动赋予一个合适的值。

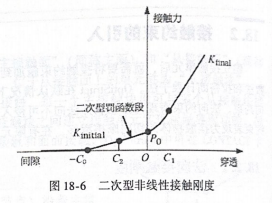
 图18-6 二次型非线性接触刚度

二次型接触刚度需要用户指定接触间隙为多少(G)时开始引人初始接触刚度K，在接触间隙为多少(C,)时开始采用二次型接触刚度，在接触穿透为多少(C)时开始使用K…。二次型非线性接触刚度如图18-6所示。二次型非线性接触刚度可在PCONT卡片的STFQDR续行定义其中C如上所述，ALPHA1=G,/特征长度，ALPHA2=(G;+C)/(C,+G)，ALPHA3=K如果用户不知道如何设置这些值，OptiStruct 提供了默认参数，可以直接采用。

切向接触刚度

库仑摩擦因其简单性和适用性而被广泛应用，它认为当切向力小于摩擦系数乘以压力(F)时，接触界面不会发生变化;当切向力等于该临界值时，接触界面发生相对滑移，且切向接触力等于该临界值。如图18-7所示可以看到切向刚度曲线为高度非线性，在静止转滑移时切向刚度为无穷大，这种突然变化将造成数值计算中迭代的收敛困难。为了解决这个问题，需要对接触刚度曲线进行改进，使其光滑化。

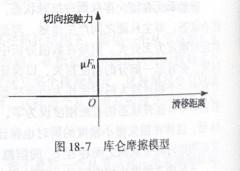
 图18-7 库仑摩模型

一种方法为引人有限的静止转滑移的接触刚度，在切向力小于F,时，允许界面间发生较小的相对位移。这种方法存在的问题是，同样的模型、不同的正压力下，接触面间静非转滑移过程中发生的相对滑移是不一样的、如图18-8n所示。为了改善这一问题，引人了第二种方法，即限制静止装滑移过程中的相对滑移量，这样同一个模型、不同的接触压力下，切向接触刚度不同。但是接触装滑移过程中发生的相对滑移量一致，结果更合理，如图18-8b所示。0ps默认采用第二方法。不同切向接触刚度模型的切换可以通过PCONT卡片上的FRICESL来设置。需要指出的是，摩擦的引人导致了非对称刚度，这将使计算收敛变慢。

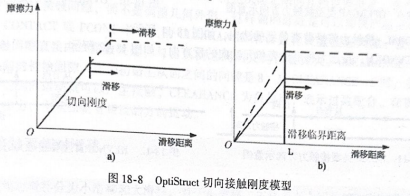
图18-8 OptiStruct 切向接触刚度模型

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。