下表简要列出了线性和非线性有限元分析之间的主要不同。关于荷载-位移关系、应力-应变关系、应力-应变度量等主要不同将在本章详细介绍。

 

 

 

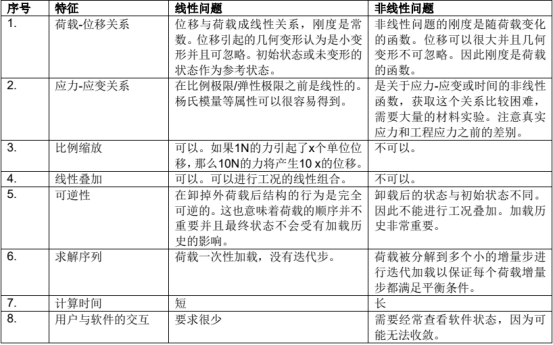
非线性的类型

有三种基本的非线性类型：几何非线性、材料非线性和接触非线性。回顾线弹性的概念——小变形并且应力与应变成比例。

 

线弹性

 

 

 

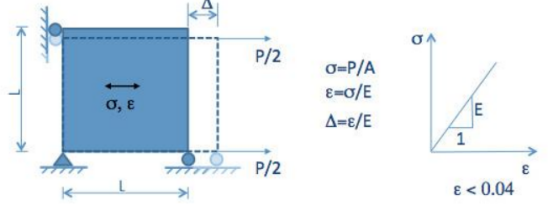
1) 几何非线性

几何非线性可能与以下几种情况有关：1)大应变 2)大转角 3)大变形

几何非线性会考虑大变形可能引起的几何截面变形（在线性静力分析中截面假定为常量）。

 

大位移也可能由几何屈曲引起。屈曲是构件在受到较大的压应力情况下的突然失效现象。实际上失稳时的压应力小于材料的根限压应力。

 

因此平衡方程必须参考变形后的结构几何重写。此外，在荷载增加的过程中，方向可能会发生变化，比如压力作用下膜结构膨胀。（参考Concepts and applications of finite element analysis; R.D. Cook et. al, 595页）

 

大位移和大转角（小应变；线性或非线性材料）

 

 

 

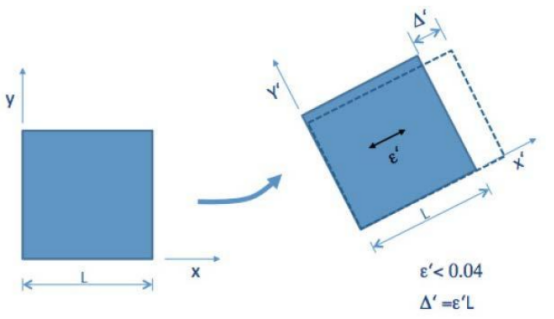
大位移、大转角和大应变（线性或非线性材料）

 

 

 

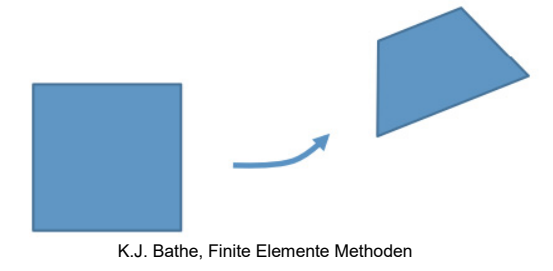
在线性FEA中，应变，如x方向应变可写为εx = ∂u/∂x，也就是说在表达式εx = ∂u/∂x + ...[(∂u/∂x)z + (∂v/∂x)z + (∂w/∂x)z]中只考虑了一次项的影响。在大位移（非线性）中，表达式的二次项也要考虑。另外，材料的应力-应变关系也不一定是线性的。

 

2）材料非线性

 

 

 

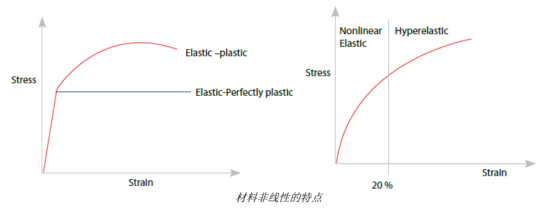
非线性材料（小位移）

 

 

 

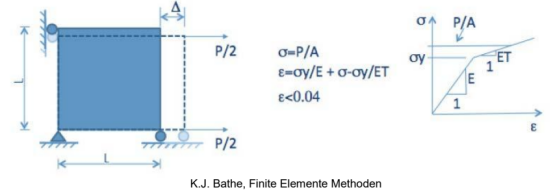
所有的工程材料本质上都是非线性的，因为无法找到单一的本构关系满足不同的条件比如加载、温度和应变率。

 

可以对材料特性进行简化，只考虑对分析来说重要的相关因素。线弹性材料（胡克定律）假设是最简单的一种。如果变形可恢复，则材料为线弹性，如果变形不可恢复，则为塑性。如果温度效应对材料属性影响较大，则应该通过热弹性或热-塑性关系考虑结构和热之间的耦合效应。如果应变率对材料有明显影响，则应使用粘-弹性或粘-塑性理论。

 

上图是一个材料非线性的示例。

材料非线性的简单分类：

1. 非线性弹性

2. 超弹性

3. 理想弹-塑性

4. 弹性-时间无关塑性

5. 时间相关塑性（蠕变）

6. 应变率相关弹-塑性

7. 温度相关的弹性和塑性

 

如果考察上图中的应力-应变曲线，则材料非线性可以分为以下几类：

1. 线弹性-理想塑性

2. 线弹性-塑性。应力-应变曲线的塑性段与时间无关，还可细分为两种：

a. 弹性-分段线性塑性（如下图所示）

b. 弹性- 真实应力应变曲线

 

 

 

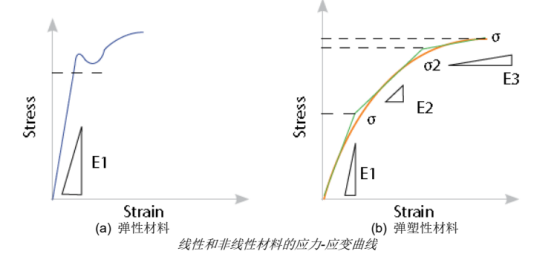
3. 没有固定屈服点的非线性弹性材料，比如进入塑性但应变远低于20%

4. 超弹性材料，比如大位移下的橡胶。典型应用是垫片材料。

 

3）边界条件非线性/接触非线性

当位移D的阶数发生变化时，说明边界条件发生改变，比如自由度的改变。

 

接触

 

 

 

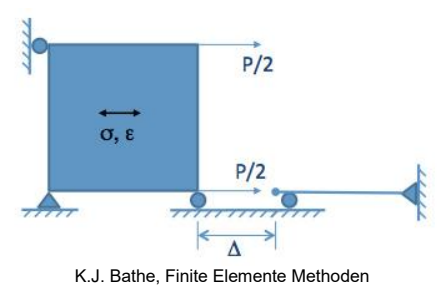
在分析中有限元模型的边界条件改变时就产生了边界条件非线性。在分析过程中边界条件可以增加或删除。这种非线性通常涉及接触，接触点随荷载的变化可能接触或分离。接触对中的荷载传递机制是一个复杂的现象。研究人员已经开发了几种理论使用接触集来描述荷载传递。有限元代码中典型的接触算法的工作原理如下：

 

首先，通过测量接触面上节点之间的距离来检查接触面分开或闭合。如果接触是闭合的，则将反力作用在接触的节点上，以防止他们互相穿透。如果接触是分开的，则这些节点之间没有荷载传递。施加到节点上的反作用力基于接触表面材料的刚度来计算。由于通过接触集的荷载传递不是恒定的，而且它需要不断检查接触的状态，这种分析不能用线性静态分析的代码实现。提高检查接触状态的频率，可以得到更准确的结果。

 

接触处理

接触处理的方法有两种：

• 罚函数法

• 拉格朗日乘数法

 

罚函数法是最常用的显式代码，在大多数 RADIOSS 接口中都有应用。拉格朗日乘数法在某些特殊情况下使用。

 

罚函数法的接触面主要基于主/从面方法。接触只能发生在一组从节点和一组主面之间。主面的定义与主面所在的单元类型有关。如果是三节点或四节点壳单元，主面就是单元表面。如果是实体单元，主面就是实体单元的一个外表面。如果是二维实体单元，主面可以是一条边。

 

与罚函数法相反，拉格朗日乘数法是纯粹的数学方法不需要物理单元（弹簧）来模拟接触。通过求解非线性系统方程来计算接触条件。因此不会由于过高的接触刚度而造成接触迭代步失败，但是由于在每个迭代步中要求解新的非线性方程组，将会消耗更多的CPU时间。这个方法的优点是可以完全阻止从节点穿透接触面（也就是说完全精确地满足接触条件），但是不能计算摩擦。