当模型某两个方向的尺寸远大于第三个方向的尺寸时，可以使用2D网格。
单元形状：四边形、三角形
用户需要知道的其他信息：另外一个方向的尺寸，例如：厚度
单元类型：薄壳单元、板单元、膜单元、平面应力单元、平面应变单元、轴对称实体单元等
实际应用：钣金类零件、面板类的塑料零件
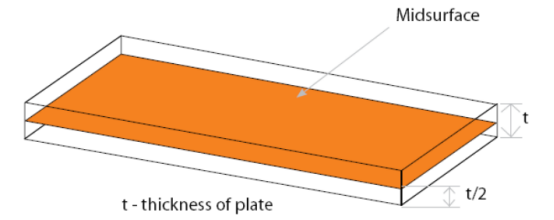
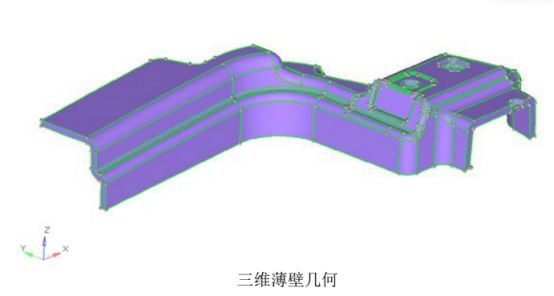
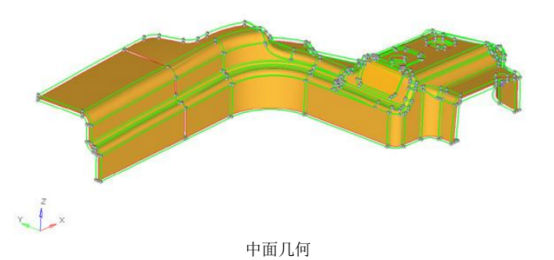
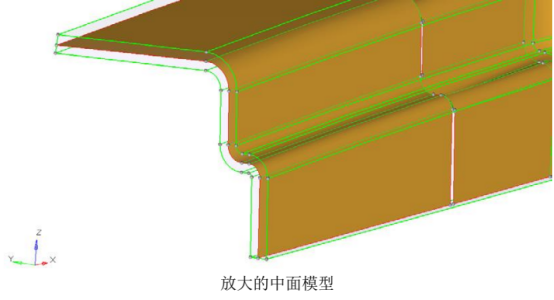
为什么2D网格要划分在中面上？
通常情况下如下图所示的薄壁3D结构，可以简化为更低维数的几何模型。这就是我们常说的中面模型。中面模型常常使用2D网格来离散划。因为模型的厚度尺寸已经赋给了2D网格，不必使用3D网格。从数学上来说，单元的厚度（由用户定义）一半定义在+Z轴方向（单元的正方向），另一半定义在-Z轴方向（单元负方向）。
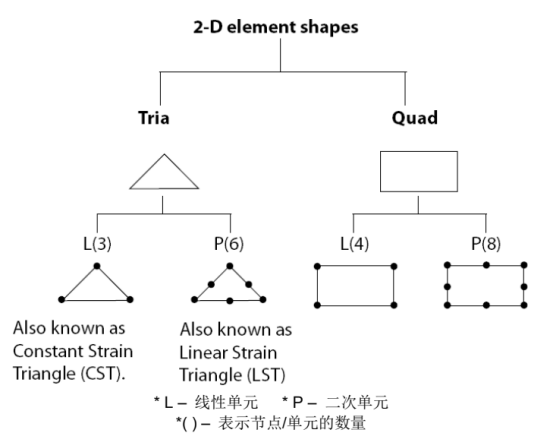
常应变单元的相关内容
关于常应变单元的说明，节选自：The CST (Constant Strain Triangle) –An insidious survivor from the infancy of FEA, by R.P. Prukl, MFT。
CST是40-50年前为有限元分析开发的第一种单元，开发之初能够很好的满足分析需求。与此同时，也开发了许多更精确的单元来替代CST。
详解
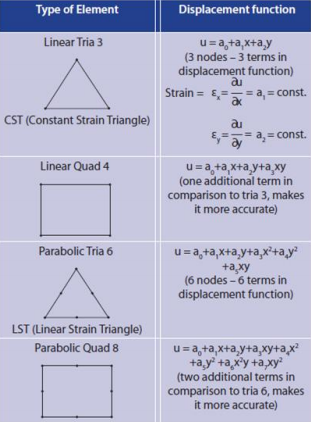
假设一个3节点平面应力单元在xy平面上的节点为1，2，3。x方向的变形为u1，u2，u3，y方向的变形为v1，v2，v3，总共六个变量。
位移函数的表达式如下所示：（使用六个常数来描述单元的行为）
这意味着什么呢？
这意味着这种单元的应变是恒定的。然而，我们知道，梁结构中，上表面受压，下表面受拉。因此，单个单元无法模拟梁结构的弯曲效应，这样什么都模拟不了。注意：因此，三节点单元对于除了平面应力和平面应变状态之外的其他应用的模拟还是可以接受的，例如：平面弯曲和热传递模拟。
解决方法：
使用四节点单元，这种单元使用8个常数来描述单元的行为：
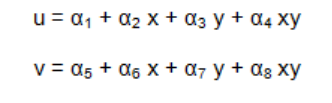
单元的应变如下所示：
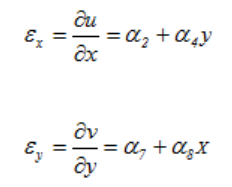
这种单元X-方向的应变是y坐标的线性函数，这比三角形单元要好多了。也可以使用包含z轴（xy平面的法线方向）转动自由度的三角形单元。
