5.1 实模态分析
模态分析提供了将多自由度系统的动力学方程转变到模态坐标q,的方法。在实模态分析中,模态特征值与振型向量均为实数。同时，动力学方程需要满足一定的阻尼条件才能进行实模态解耦下面通过一些简要公式来阐述这些问题。
5.1.1 基本方程
结构动力学响应在模态空间中的分解，可以将模态坐标q;合并成列向量q=|q,,q,,…,q即模态坐标，也称为广义坐标。将模态振型向量(pli=1,2,3,…合并成矩阵形式，Ф=[4,4,4,…]，模态振型矩阵 φ为所有特征向量。 的集合。
那么位移u的时域及频域表达式(4-16)可写成矩阵形式：
u(1)=Фq(t),u(s)=Фq(s)将式(5-1)代入频域动力学方程式(4-14)，并在方程两侧同时乘以"，得到s'ФMФq(s) +s Ф'CФq(s) + Ф™KФq(s) =Ф f(s)(SM+s℃+〖)g(s)=f(s)
这是模态空间下的频域动力学方程。其中：
1)M-ФMФ，称为模态/广义质量矩阵。
2)-ФCФ，称为模态/广义阻尼矩阵
3)又-Ф"KФ，称为模态/广义刚度矩阵
4)-,称为模态/广义激励力(列)向量。
在模态空间中，各个模态坐标q的运动是相互独立的。因此，式(5-3)中的矩阵M、、必须都是对角矩阵，
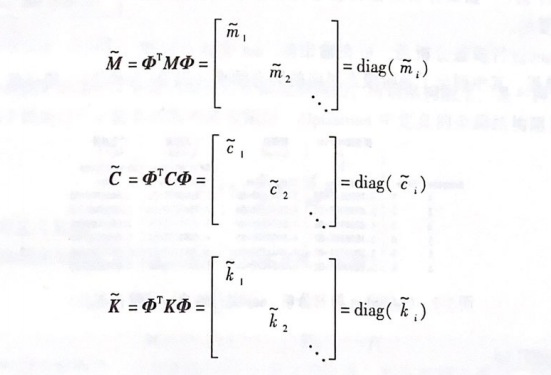
式中，|i=1,2,…|为模态阶次，最大的模态阶次与有限元中的自由度总数相等;m,为模态质量;
c,为模态阻尼;,为模态刚度;diag()表示仅矩阵主对角线元素不为零的对角矩阵。实模态分析的核心问题是如何获取满足式(5-4)的模态矩阵。如果矩阵M、C、K是任意的，并不一定能找到满足该要求的解。事实上，只有M、C、K为对称矩阵，且阻尼C满足一定条件时，才满足实模态的要求。
本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。
