HyperWorks进阶教程：OptiStruct模态振型及频率

实模态振型最初是从无阻尼结构中推导出来的。忽略外激励的作用，频域动力学方程简化为

SMu(s)+Ku(s)=0或Ku(w)=ωMu(ω)这是一个典型的广义矩阵特征值问题，可求得实特征值入，和实特征向量4;。特征值λ,对应于结构的固有频率ω,，特征向量,对应于结构的模态振型

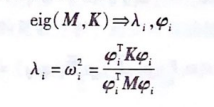
由于任意特征向量，在缩放任意倍数后依然满足式（5-6），因此为保证模态振型数值的位移性需要规范化特征向量。在OptiStruct中默认采用“广义质量归一化”的方式决定模态振型的数值。

采用质量归一化标准后，模态质量矩阵M变为单位矩阵，模态刚度矩阵变为的对角矩阵。

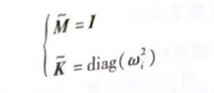
图5-1所示为典型模态分析在.fem文件中的工况定义。一般只需要在工况定义中设置模态分析方法卡片METHOD，以及对应的结构变界条件SPC。如果分析的是自由结构的模态，那么SPC字段也是不需要的。

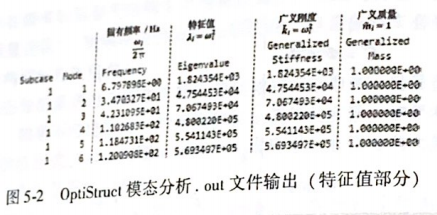
用OptiStruct进行模态分析后，可在输出的.out文件中找到图5-2所示的结果。其中列出了各阶段模态对应的固有频率（以Hz为单位）、特征值、广义刚度、广义质量。

5.1.3 比例阻尼

除了无阻尼结构以外，比例阻尼结构也满足实模态解耦。比例阻尼即阻尼矩阵是质量与刚度矩阵的线性组合形式，通常指的是瑞利(Rayleigh)黏性阻尼。在OptiStruct 中，比例阻尼是通过参数PARAM.ALPHAI与PARAM，ALPHA2 进行定义的。

C=α,M+α,K(5-10)比例阻尼结构的模态振型矩阵Φ与无阻尼情形的计算结果是完全相同的，这可由比例阻尼的定义得到。此时，模态阻尼矩阵C依然为对角矩阵。

Ã=ф(α,M+α,K)Ф=α,I+a,〖因此在模态空间的动力学方程依然是解耦的。时域方程表达为

(5-11)

战

频域方程表达为

¤(±)+(α,I+α,〖)¡(t)+〖q(t)=f(t)¤,(t)+(α,+a,@)á,(1)+w?g (t)=广(t)

(5-12)

(S]+s(a,1+a,〖)+〖)g(s)=f(t)

(-@°+jω(α, +a,w¡)+@)q(@)=f(w)(5-13)代入单自由度简谐激励振动的频域解，c;=α,+a,“,，”,=1，%,=心，于是各阶模态的阻尼

或

比为

a,+, w’5:=-2 0:2、尼m

(5-14)

各阶模态的振动频率为

w,= √-fmiw

(5-15)

这里ω，的下标d表示 damping，意为含阻尼时结构的振动频率，需要注意的是，如果在 0iStnuct中采用比例阻尼进行仿真，那么各阶模态的阻尼比是不相同的。从式(5-14)可知，随着模态频率,的数值变化，阻尼比,是变化的。在模态频率比较高时模态阻尼比6与模态频率ω,近似为线性增长的关系。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。