HyperWorks进阶教程：OptiStruct结构阻尼

采用全局结构阻尼的动力学方程也是满足实模态解耦的。所谓结构阻尼，是一种因位移产生的能量耗散，有别于因速度产生能量耗散的黏性阻尼。Optistruct中定义的全局结构阻尼也是一种比例阻尼：

C=j.EK=EK。

式中，g是一个自定义常数。将这种形式的阻尼矩阵代入时域及频域动力学方程，得到

Mü(t)+Kù(t)+Ku(t)=f(t)。

SMu(s)+(1+j·g)Ku(s)=f(s)(5-18)可以看到，时域方程中是一个随激励频率ω变化的矩阵，而在频域方程中，阻尼合并到刚度项，成为一个复刚度矩阵(1+j·g)K，与激励频率ω无关。

因此，在Optistruct中定义结构阻尼有些特殊。在频率响应分析类型中，只需要采用PARAM，G定义参数即可;而在瞬态响应分析类型中，需要额外采用PARAM，W3定义式中的参数。将式(5-17)与式(5-18)在实模态空间中进行表示。此时，时域方程为#(蟄導祗Ç蜻硫丈烯+長〖ú()+〖q(t)=f(t)莓,(t)+.㎡á (t)+©q,(t)=广(1)(

频域方程为

sq(s)+(1+j·g)〖q(s)=f(s)(s+(1 +j·g)@)q;(s)=F(s)可求解式中每一阶模态的复数方程，得到对应的特征值：

-0,a±j@;d

式中、、为结构阻尼情形下的振动频率，w略大于a:8,为各校态坐标的阻尼系数，该数价。0WS:““发模态分析输出的.“文件中表示为“dmpimg”:6,为将结构阻尼等效为黏性阳尼时的。尼比。在小限尼协况下，一8，6一8/2。因此，如果采用PARAM，G的全局结构阻尼进行份：

那么各阶模态阻尼或阻尼比是完全相同的。图53直观地给出了比例阻尼与结构阻尼两种形式的模态阻尼比曲线。可以看到，采用口lei阳尼进行计算时，在极低频和高频段有很大的振动屏蔽效应，而采用结构阻尼进行计算的各阶模态的阴尼是相等的。

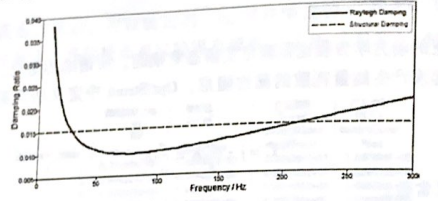
图5-3 0puiStnuct模态阻尼比(比例阻尼、全局结构阻尼)

5.1.5 SDAMPING阻尼

除此之外，实模态解耦的情况还存在于 SDAMPING 阻尼类型，即直接定义各阶模态的阻尼比在Optistruct中，通过TABDMP1卡片定义阻尼比随频率变化的曲线(ω)，由工况控制卡片SDAMPING 进行选取。这样第i阶模态的阻尼比就可以依靠查表的方式被直接定义为:6:=(w;)。

于是式(4-17)与式(4-18)中的广义模态阻尼为;=26:;。采用 SDAMPING 阻尼方式时，模态振型矩阵与无阻尼情形完全一致，而阻尼比曲线((ω)可以根据试验测试进行标定。在Optistruct仿真应用中，SDAMPING是最灵活的一种阻尼使用方式相较于比例阻尼或结构阻尼，它可以更准确地表达阻尼效应。在具备试验测试条件的情况下，推荐采用 SDAMPING 方式定义有限元模型的阻尼。

模态以外，其余的模态频率均大于0，此时结构发生弹性形变，有弹性势能产生，称为弹性模态依据上面的定义及描述，刚体模态4。满足弹性势能为0，即

9.Ky =0=k。=oK华=0

即无须外力作用，结构就能产生静力位移。刚体模态频率w。=0，刚度矩阵K非满秩

一个结构处于无约束的自由状态时，共有6个独立的刚体模态振型4。，分别对应3个平动和3个转动状态。有限元数值计算中，获取的刚体模态通常为平动和转动的线性组合，且由于数值精度问题，获取的刚体模态频率一般不严格为0。如图5-4所示，刚体模态频率通常远低于第一阶弹性模态频率，可认为近似等于0。

在Optistruct实际应用中，常利用模态分析的刚体模态数目来检查建模错误。建模正确的情况下，对于充分约束的结构，应当确保不存在刚体模态。而对于完全自由的单个结构，应该确保刚体模态仅为6个。例如，如果出现固支位置遗漏SPC、应相连的部件未进行连接、连接单元刚度为0等情况，那么单个结构的刚体模态数目将大于6，应当通过补充必要的连接以及修正SPC 等方式修复模型。

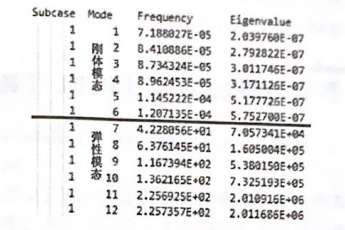
图5-4 0iStruct 模态分析:刚体模态频率

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。