几何非线性

现实生活中，刚度[K]是位移[d]的函数(记住: 线性分析中[K]是不变的，独立于[d])。这意味着在几何非线性分析中，在预定义的位移后，刚度矩阵 K 需要重新计算。例如在屈曲发生后，几何刚度将显著的改变。为了计算得到正确的结果，所以应该考虑变形后的几何。

我从事几何非线性的工作数年，也有同样的问题。起初我以为只是位移和转动的大小决定了是否几何非线性问题。比如，如果变形小就是线性问题，大就是几何非线性问题。

然而，几何非线性并不仅限于大位移和大转动。如果一个悬臂梁在末端承受力，它的位移只有其长度的 10 分之一，可以认为它是线性的。

我的意思是在这种范围的变形下，你可以通过线性分析来得到较好的近似值。但是一个同样长度的简支拱，在同样的受力下，在突弹跳变改变形状之前，它的末端即使位移仍然很小，但确是高度非线性的。另外一个例子是，壳的属曲，虽然初始变形很小但是经历的是一个非线性的行为。

简而言之，我相信需要试验验证几何非线性而不是光靠看来判断。如果这个案例是关于屈曲和分岔分析，因为屈曲(突弹跳变)在只作用膜和轴力的小位移情况下即可发生，绝大多数情况下和几何非线性有关。

观察结构，判断变形是否由弯曲和轴力产生的。如果是轴力引起的，多半是几何非线性。如果是弯曲引起的并且变形较大，也是几何非线性问题。当然最好的方法是进行几何非线性分析，并且和线性分析对比，如果差别较大，当然就是几何非线性问题。C. Contact-这种类型的非线分析用在部件之间的物接(承和过配合等)。

动力学分析

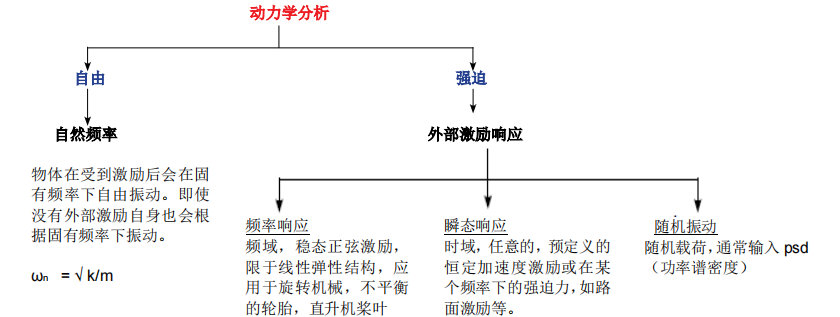
在线性静态分析中，求解的方程为 F = K*u。而动力学分析是基于另外的方程式：[M] x + [C]x' + [K] x = F(t)

X‘’= d2x /dt2 =加速度，x'= dx /dt =速度，x =位移

[M] x= 0,[C]x” = 0,[K and F(t) = 常值

[M] x = 0,[C]x' = 0,[]是的函数,F(t) =常值

F(t) = 0,[C]x' = 0 and [M],[K] =常值

以上术语都会用到

实际应用：自然频率是部件的基本设计属性。而强迫振动适用于部件受到随时间或频率变化的力，位移，速度或加速度激励

线性屈曲分析

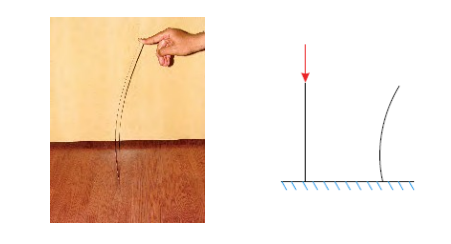
一些关键方面：

l适用于只有压缩负载

l纤细的梁和饭金件

l弯曲刚度<<<轴向刚度

l大侧向变形

软件计算输出结果：负载的临界值。

实际应用：土木工程中常用。机械工程中应用在真空容器，长变速杆分析等。