Optistruct超弹性材料（1）超弹性材料模型有哪些？

对于橡胶、海绵、泡沫等材料，应变可达到1，甚至5，但是卸除载荷后应变可以完全恢复，应力、应变之间呈现出非线性，应变能取决于变形的最终状态，而与之前的变形历史无关，这类材料可以用超弹性材料本构描述。

在应变为、应力为σ的状态下，给应变一个微小的变化 de，相应的应变能微小变化为

dw = ode

同时应变能w的变化还可通过微分表示为

如果某种材料的应变能能用一个势函数表示，就称这种材料为“超弹性材料”。应变能只和最终状态的应变有关，和变形路径没有关系。当势能函数w取为正定二次齐次函数时，其对应于线性材料。材料是各向同性时，应变能函数是应变张量不变量的函数。不同的学者提出了不同的势能函数，对应于不同的超弹性模型，下面列出了常用的超弹性模型。

1）通用多项式形式的超弹性模型，也称为Mooney 模型。

式中，N 为畸变能多项式阶数;N,为体积变形能多项式阶数;C为材料常数;p、q为多项式指数;7、7,分别为应变的第一、第二不变量;D,为体积变形相关的材料参数;」为体积应变。

2) Mooney模型中，N,=N,=1时，退化为Mooney-Rivlin 模型。

3）Mooney模型中，q=0，N,=1时，为退化的多项式模型。

4）Mooney模型中，N,=N,=1,q=0 时为 Neo-Hooken 模型。

5）Mooney模型中，N,=3，N, =1，q=0 时为 Yeoh 模型。

6）ABOYCE模型表示为

7）Ogden模型表示为

超弹性材料参数获取

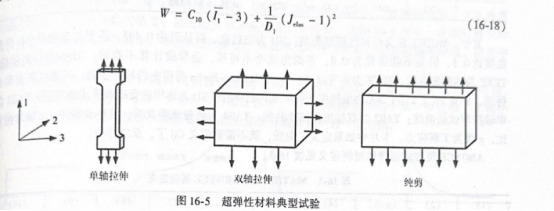
超弹性模型中的材料参数可以通过简单试验得到，最常用的是单轴拉伸、双轴拉伸及纯剪，如图 16-5 所示。

在单辅拉伸中，采用标准试件、一端加载，应力状态为a;=0,=0，考虑到材料不可压,1、2.3方商的伸长率满足S二小三VAT。在纯剪试验中、取宽而薄的橡胶片，固定在两块金属板上、3有作用拉伸载荷。两块金属板的变形可略去，而橡胶片又很宽，因而中央部分可近似地有大，1考虑材料不可压，、A,À,=1。在等双轴拉伸实验中，取一正方形试件，在1、2方向拉伸。对等双装拉伸有σ,=0;、0,=0，入,=À:，À,=六。以上三种试验的超弹性材料应变能都可以只用入,来表示，以 Neo-Hooken 模型为例：

1）在单轴拉伸中，应变第一不变量可表示为

将应变能函数对主伸长求导得到名义应力S：

2）在双轴拉伸中，应变第一不变量可表示为

将应变能函数对主伸长求导得到名义应力S：

3）在纯剪中，应变第一不变量可表示为

将应变能函数对主伸长求导得到名义应力S：

通过试验可得到三条名义应力相对于主伸长的曲线，采用以上表达式拟合三条曲线，得到最佳材料系数C。D,可通过静水压力试验曲线得到。至此该材料完全确定。其他超弹性模型的材料系数可采用同样的方法得到。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。