Optistruct非线性隐式动力学分析

动力学分析根据其刚度矩阵是否为位移的函数、阻尼矩阵是否为速度的函数可分为线性动力学及非线性动力学。线性动力学在前面章节已经介绍，由于系统是线性的，可使用叠加原理，所以多采用模态叠加法对方程进行求解。也可以采用直接积分法进行求解，但是计算效率不如直接积分法。对于非线性动力学问题，模态叠加法就不再适用，只能采用直接积分法。

根据对时间积分采用的插值算法的不同，又分为显式积分方法和隐式积分方法。其中，显式积分方法以中心差分法为代表，其特点是条件稳定、时间步长小，适用于高速碰撞，Altair产品中的Radioss 就是一款专业的显式动力学求解软件。

隐式积分方法无条件稳定，时间步长根据精度要求决定，求解过程需要对方程组进行迭代，适用于低速碰撞。OptiStruct提供了隐式动力学求解方法。本章主要介绍OptiStruct隐式动力学求解的相关内容。

隐式动力学理论基础

OptiStruct隐式动力学采用的积分方法为广义a方法及后退的欧拉方法，其理论简单介绍

如下。

广义α方法

广义α方法的平衡方程离散如下

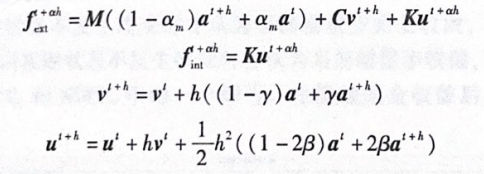
式中，M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;“为外载;“为由于结构刚度产生的内力;“为位移;v为速度;a为加速度;t为前一个时间步;t+h为当前时间步;t+ah 表示对于任意量z，1+wh 时刻的值由t及t+h时刻的值线性插值得到。

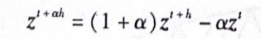
从上面的方程可以看到，广义α方法有四个归一化的参数:a、B、y及a_。当a_=0.0时，该方法退化为HHT-α方法;当a=a_=0.0时，退化为Newmark-B方法。a、a、B的取值范围为

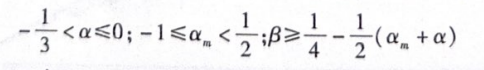
 式(20-3)和式(20-4)中，、β可由a及a,得到，OptiStruct中默认值为a_=0.0,α=-0.05,

即默认采用 HHT-α 方法。

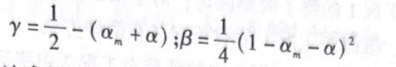
广义a方法采用牛顿下山法求解非线性方程，对每个增量步通过选代(j为迭代数)得到位移量 Δ=㎡-"'，从而推导出速度及加速度，其中的下标为迭代数。

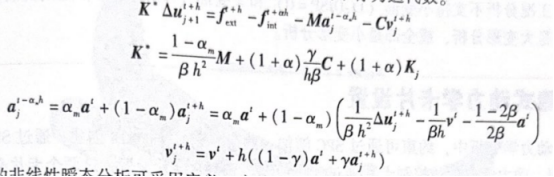
大多数的非线性瞬态分析可采用广义α方法，通过α、β、y及a_调整数值阻尼,当α及α非零值时，可滤去高频响应。

后退的欧拉方法

在后退的欧拉方法中，平衡方程的离散如下：

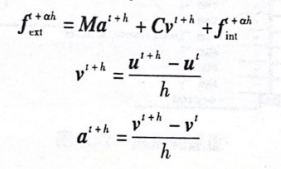
后退的欧拉方法同样采用牛顿下山法求解非线性方程，对于每个迭代步的位移增量 Δu**=u*可通过下面的表达式得到。

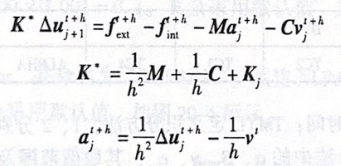
后退的欧拉方法适用于准静态分析，比如后屈曲分析。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。