多轴疲劳分析的非比例硬化和弹塑性应力修正

在比例加载过程中，应力主轴不发生变化，最大剪应力面固定在一个平面，晶格滑移带在这个平面萌生并扩展。在非比例加载过程中，最大剪应力面在加载过程中不断发生变化，导致在一点产生了多个晶格滑移面，这些晶格滑移面相互交错、相互作用，犹如在晶格滑移处打了一个结，晶格滑移相对来说变得困难，如图23-5a所示。相对于比例硬化，非比例硬化引人了额外的硬化效果在相同的塑性应变下应力更高，其中相位相差90°的非比例加载硬化效果尤为突出，如图23-56所示。

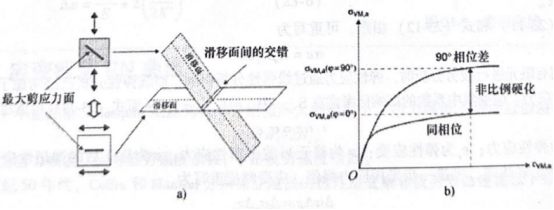
图23-5 非比例硬化

在比例加载下可以得到材料的循环应力应变曲线，非比例加载下材料的循环应力应变曲线可以通过对比例加载的循环应力应变曲线修正得到：

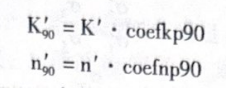
式中，cockp90及coemp90可通过MATFAT卡片EN续行的 Cogkp90、cogmp90定义，coekp90 的默认值为1.2，coefnp90 的默认值为 1.0。

弹塑性应力修正

在低周疲劳分析中，结构分析得到的是线弹性应力结果需要根据弹性应力结果修正到弹塑性应力结果。

（1）非比例加载下的弹塑性应力修正

在非比例载荷下，0iStruct采用Jiang-Sehioglu 弹塑性模型结合滞回曲线及Neuber修正，将弹性应力修正到弹塑性应力。由于Jiang-Sehitoglu 非常复杂，感兴趣的读者可参考相关文献，这里不再详述。

（2）比例加载下的弹塑性应力修正

在比例加载作用下，应力主轴不发生翻转，此时就不需要采用复杂的Jiang-Sehioglu 模型，而是采用Hofmann-Seeger方法进行修正。当FATPARM卡片上MAXLFAT=YES，CHK=YES目FATEVNT卡片上只引用了一个静力工况时，将采用Hofmann-Seeger应力修正。Hofimann-Seeger 应力修正有以下几个假设。

1）平面应力假设，面外主应力为0。

2）主应力及主应变轴不变。

3）面内主应力比不变。

Hofimann-Seeger应力修正的主要步骤如下。

1）通过弹性应力计算带符号的 Mises 应力、应变

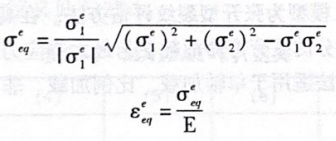
式中，σ、σ;为弹性第1、2主应力;σ”为带符号的 Mises 应力;E为杨氏模量。

2）通过 Neuber 修正及循环应力应变曲线得到弹塑性应力应变。

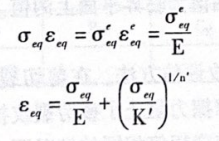
式中，σ、e_为弹塑性等效应力应变。

3)计算塑性模量 H。

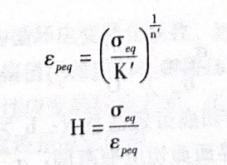
式中，e为等效塑性应变。
（4）计算主应力。

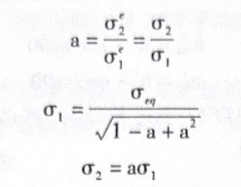
式中，0、0,为修正后的第1、2 主应力。

5）计算主应变。

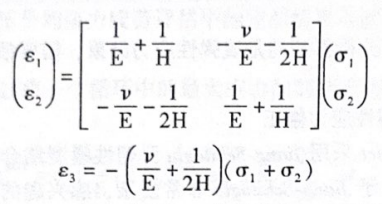
式中，,、E,、ē,为修正后的第1、2、3主应变;v为泊松比;H见式(23-21);E为杨氏模量。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。