滞回曲线和应变疲劳EN曲线

滞回曲线

循环应力应变曲线并不是真实的加卸载曲线，材料的加载、卸载并不沿着循环应力应变曲线，而是沿着图23-3中的闭环变化，图23-3中的闭环称为“回环”Massing理论提出滞回环的半支和循环应力应变曲线的上半支形式是一样的，只不过是用(Ao,As)替代了(σ,e)，其中，o=2σ，Ae=2ε。替换后滞回曲线的表达式为

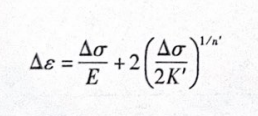
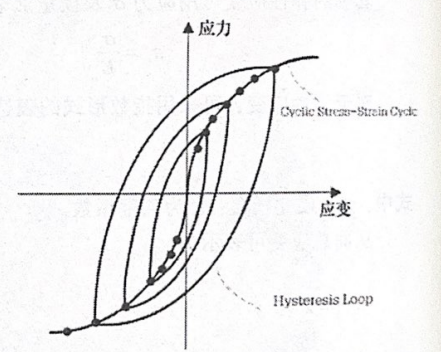
图23-3滞回曲线

应变疲劳 EN 曲线

大约一个世纪前，Basquin 观测到在应力幅值不大的情况下，应力幅值与寿命近似遵循o =o'(2N)式中，σ,为应力幅值；σ为疲劳强度系数；b是疲劳强度指数。

19世纪50年代，Con 和 Manson 分别独立地提出塑性应变幅和疲劳寿命遵循以下指数关系：

E"=ε'(2N )式中，e为塑性应变幅值；e为疲劳延性系数；c为疲劳延性指数。Momow 综合了以上两种方法，通过将 Basquim 表达式转换为弹性应变得到弹性应变幅值为

6-后=-(2N)'

将其和 Con-Manson 表达式合并，得到

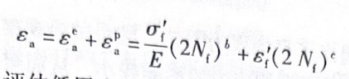
式中，8,为应变幅值。该式用来评估低周疲劳EN曲线如图23-4所示。EN曲线可通过 MATFAT卡片上的EN续行定义，其中,σ通过S定义,c通过所定义，指数6、c通过卡片上的字段 B、C定义。

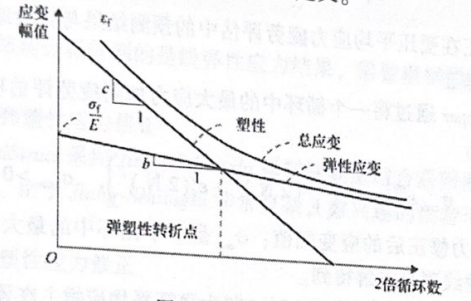
图23-4 EN曲线

单轴疲劳分析

Neuber 应力修正

Neuber 应力修正是广泛应用的一种从弹性应力应变修正到弹塑性应力应变的方法。在工程实际中，通常结构整体上处于弹性，在缺口根部由于应力集中，存在局部塑性。局部应力可由名义应力乘以应力集中系数得到，同样的局部应变也可以由名义应变乘以应变集中系数得到：

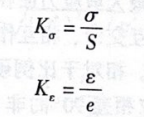
式中,σ为局部应力；ε为局部应变；K为应力集中系数；S为名义应力；e为名义应变；K为应变集中系数。

将式(23-11)和式(23-12)相乘，可重写为

σε =K K Se

(23-13)在采用有限元进行疲劳分析时，弹性应力通过线弹性分析得到，而线弹性分析已经考虑了几何因素的影响，即应力、应变集中系数的影响已考虑在S、e中，故K。K,=1，从而式(23-13)可重写为

OE =O.E.式中，σ.为弹性应力；e,为弹性应变；σ为修正后的弹塑性应力；ε为修正后的弹塑性应变。这就是Neuber 修正表达式，可进一步采用应力幅值、应变幅值重写为

AoAE =Aσ E

该表达式结合滞回曲线表达式可从弹性应力应变幅值修正到弹塑性应力应变幅值

平均应力修正

受压平均应力使疲劳裂纹闭合，受拉平均应力使疲劳裂纹张开，平均应力显著影响疲劳寿命。低周疲劳分析中较常用的有Morou平均应力修正及SWT平均应力修正，分别介绍如下。

（1）Morrou平均应力修正

Morow 首次针对应变疲劳提出了平均应力修正。结合试验观察，在塑性应变较小时，平均应力的影响较显著、在塑性应变较大时，平均应力的影响较小，从而可将平均应力~的影响添加到弹性应变项。Morrou平均应力修正公式为

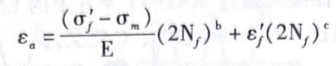
Morrouo平均应力修正在受压平均应力疲劳评估中的预测结果与试验结果吻合较好

（2）SWT平均应力修正

Smih、Watson和Topper 通过将一个循环中的最大应力加到疲劳评估项来考虑平均应力的影响该平均应力修正可表示为

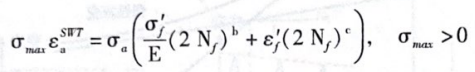
式中，ε为考虑平均应力修正后的应变幅值；σ-是一个循环中的最大应力；σ可通过 Neuber 应力修正及循环应力应变曲线联合求解得到。

当一个循环中的最大应力小于或等于0时，即为受压平均应力，在该循环导致的损伤为0，这一点和实际情况有一定的出入。在受拉平均应力疲劳评估中，SWT方法偏保守。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。