本章详细介绍低周疲劳的分析流程，以及在OptiStruct中进行低周疲劳分析的相关设置。
单调载荷下的应力应变曲线
弹塑性材料在单调载荷作用下的真实应力应变如图23-1所示，OA阶段为弹性段，A点为屈服极限，超过A点以后材料进人塑性段，继续加载至C点，材料破坏。在进入塑性段以后，材料的应变包含两部分
E=Ee+Ep
式中，ε为全应变;s.为弹性应变;s为塑性应变，其中的弹性应变可用应力σ及模量E表示为
6.-%对于塑性应变，可采用指数形式的表达式拟合得到：
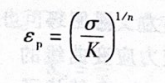
式中，n为硬化指数;K为强度系数。从而总应变可表示为
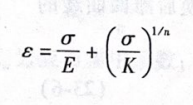
循环载荷下的应力应变曲线
在循环载荷作用下，材料可表现出四种状态
1）稳定响应。
2）循环硬化。
3）循环软化。
4）取决于应变幅值，可能是循环硬化，也可能是循环软化。
循环硬化和循环软化现象如图23-2所示。在循环硬化过程中，应变幅值保持不变，应力幅值不断变大;在循环软化过程中，应变幅值保持不变，应力幅值不断减小。一般来说，这种循环硬化、循环软化不会一直持续下去，一般会经过不多的循环达到稳定状态。将应力、应变绘制在一张图中，在材料响应稳定后，可得到一个闭合曲线。将不同应变幅值下稳定后的闭合曲线绘制在一张图中，将峰值点用一条曲线连接起来，就可以得到循环载荷下的应力应变曲线，如图233所示这条曲线和单调拉伸的曲线形状类似，可表示为
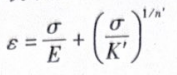
式中，K'为循环强度系数;n'为循环应变硬化指数。
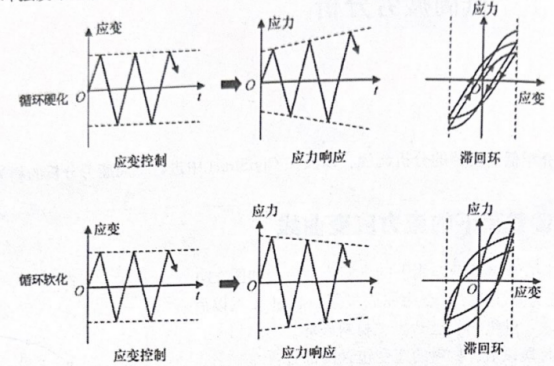
图23-2 循环硬化及循环软化
（内容、图片来源：CST仿真专家之路公众号，侵删）
版权与免责声明：
凡未注明作者、来源的内容均为转载稿，如出现版权问题，请及时联系我们处理。我们对页面中展示内容的真实性、准确性和合法性均不承担任何法律责任。如内容信息对您产生影响，请及时联系我们修改或删除。
