AcuSolve流固耦合解决方案

1. 流固耦合简介

流固耦合，Fluid-Structure Interaction（简称FSI），指的是可移动、可变形的结构和内流、外流之间的相互作用；这种相互作用可以是最终趋于稳定的，也可以是按一定的周期振荡的。如果是振荡的相互作用，那么结构体诱发的应变导致结构运动，从而减少应变量，随后结构体回复到前一个状态，上述过程不断重复。

从理论上来讲，流体域和固体域有各自的控制方程，无法独立求解，也无法显示地消去其中一个域的变量，因此只能通过相互耦合求解。广义的流固耦合分为两大类。第一类耦合中，流体域和固体域全部、部分重叠在一起，最典型的例子就是渗流问题，由于流体的渗透压作用，固体的受力也会发生相应的变化。第二类耦合指的是流体和固体仅在边界上相互作用，这类耦合广泛应用于动力学问题和传热学问题，比如瞬态流场中梁结构的动力学响应（图1）。

 

 

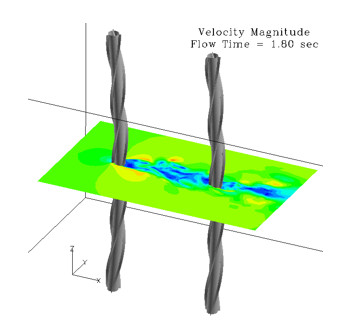
图1. 流固耦合动力学：瞬态流场中梁结构的动力学响应（AcuSolve计算结果）

 

CAE行业中通常提到的流固耦合为狭义的流固耦合，即上述的第二类流固耦合。而这种只在流固交界面上传递数据的耦合方式又可细分为简单的载荷映射、实用流固耦合（P-FSI）、直接流固耦合（DC-FSI）和流体/多体耦合（CFD/MBD）。其中载荷映射的实质是解耦的分步计算，即CFD求解器和结构求解器分别独立计算，只在流固耦合边界上做数据传递；这种方法适用于非紧密耦合的问题，比如热固耦合，流体求解器计算温度场，结构求解器计算固体内的热变形和热应力。实用流固耦合（P-FSI）和直接流固耦合（DC-FSI）考虑的是柔性体的动力变形，其中P-FSI又称单向流固耦合，AcuSolve独有的技术，本质是一种基于模态叠加以预测线性材料小变形的结构运动的方法；而DC-FSI又称双向流固耦合，即每个时间步内进行实时耦合，载荷和位移交替迭代。最后一种流体动力学与多体动力学的耦合，用来考虑更复杂的多自由度刚体运动，也可以同时考虑整个运动系统中的柔性体变形。本方案中主要介绍的是针对流致振动问题的P-FSI和DC-FSI两种方法。

2. 实现流固耦合的关键技术

无论是P-FSI还是DC-FSI，其耦合的本质都是流体和固体间的数据传递。具体来说，流体运动给固体施加载荷，固体接收到流体载荷的数据并计算固体的变形情况，而固体变形又导致了流场几何的改变，因此输出位移的数据传递给流体，从而形成了循环迭代（图2）。

 

 

图2. 流固耦合中的循环迭代

 

流固耦合在数值计算方面难的度体现在坐标系的统一，流体通常使用欧拉（Euler）坐标系，而固体使用的是拉格朗日（Lagrange）坐标系，AcuSolve通过任意拉格朗日-欧拉法（ALE）实现网格运动，在整个运动过程中无需进行网格重构。ALE是一种统一化的拉格朗日-欧拉坐标系，其优点在于：可以在耦合边界上保证网格和运动边界的一致；继承了欧拉坐标系在计算流体问题时的便利性；强大的网格变形能力是流固耦合求解能够收敛的一个重要因素。值得一提的是，大多数基于有限体积法的CFD求解器对单元质量极其敏感，如果单元的扭曲度高，求解器会无法计算。AcuSolve作为有限单元法的CFD求解器，其一大优势在于，对高度扭曲的单元有极佳的容忍性，求解精度不依赖于网格质量（图3）。

 

 

 

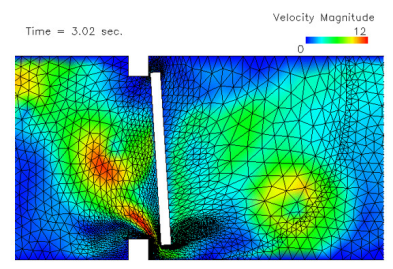
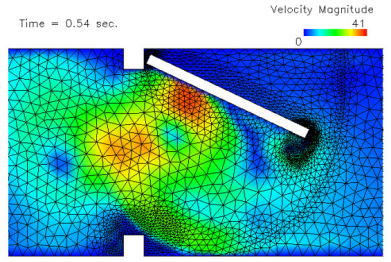
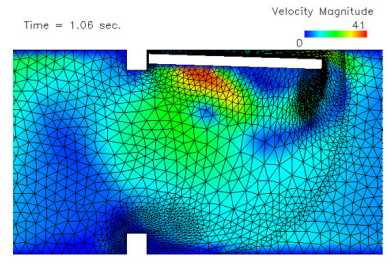
图3. AcuSolve中的ALE网格运动：局部高度扭曲的单元不影响计算的收敛性和精度

 

除了ALE网格运动，多步迭代耦合（Multi-Iterative Coupling）也是流固耦合的关键技术之一。传统的CSS（Coupled Sequential Staggered）时间迭代方法容易导致计算的不稳定，特别是流体和固体的质量密度比较高的时候。AcuSolve在2008年年独创的MIC方法有效地扩大了稳定区间，并将此方法成功运用在了与主流结构非线性求解器（如RADIOSS、Abaqus、Nastran）的直接耦合计算中。

代码耦合接口（Code Coupling Interface）是流固耦合中又一常见的技术壁垒，一般来说可通过FIFO、pipe、TCP Socket等方式实现数据传递。直接流固耦合中的双向数据传递，通常需要第三方软件来实现，而在HyperWorks平台中流体求解器AcuSolve和结构求解器RADIOSS的实时数据传递是不需要通过第三方软件来实现的。

 

3. AcuSolve中的流固耦合

3.1 实用流固耦合

实用流固耦合（P-FSI）是Acuolve独创的一种基于结构模态的耦合方法。从动力学基本方程出发，并基于线性结构变形的假设，以及模态数足够代表结构的动力学特性的假设，将力学系统映射到特征空间中，继而求解简化系统的常微分方程组。P-FSI的基本流程如下：

- 第一步：建立结构有限元网格，在结构求解器中建模并计算n阶模态，得到模态文件；

- 第二步：建立流体网格，导入模态文件，将特征向量投射到流体模型表面的节点上；

- 第三步：在流体求解器AcuSolve中设置流体计算参数，并根据读入的ODE系数和投射的特征向量求解流场和结构表面的线性变形。

 

需要注意的是，流体模型和解构模型几何表面要重合，但是单元节点不需要一一对应（图4）。在导入模态文件时，AcuSolve会自动提取所需要的模态信息（质量、刚度、阻尼、每个模态的特征向量）等信息，并对流体网格进行自动插值，将这些信息投射到流体网格中，赋予耦合边界固体的性质。

 

 

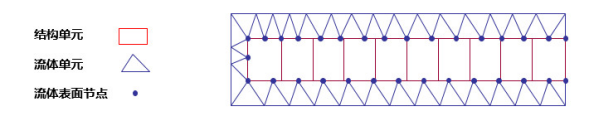
图4. 结构单元的节点和流体单元的节点无需一一对应

 

AcuSolve在每个时间步内的求解过程包括两个方面：根据流场的结果，提取流固耦合面上的节点力，乘以特征向量得到特征系统中的ODE力，再通过时间推进求解模态响应；根据求得的ODE结果和特征向量结果，求解并施加节点位移边界条件和节点速度，以及变形网格中的流动方程。

P-FSI的优势有以下几点：1）流体求解器和结构求解器分别独立运行，两者不需要实时耦合，因此两者的时间步长和总物理时间的设置均无需一致，流体的网格尺寸也不受FSI的限制；2）和其他方法相比，因为不考虑高波数模态，所以计算更稳定；3）前处理时间短，CPU计算时间也短，因此更高效。

考虑到P-FSI的局限性，其适用范围如下：1）只适用于材料小变形的线性结构问题；2）出于实用性的考虑，一般只求解低阶模态；3）只支持简化的点、面接触模型，不支持部件之间的接触模型。

 

案例1：P-FSI在风电行业中的应用 – 叶片气弹性

 

 

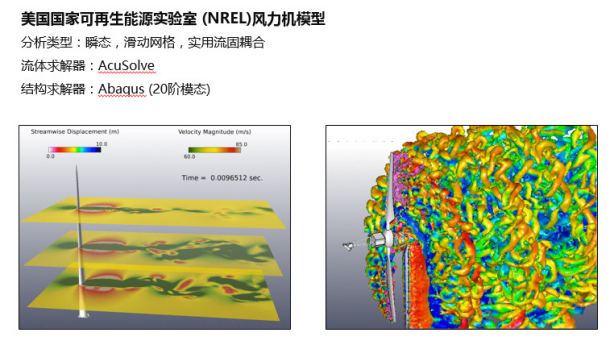
案例2：P-FSI在F1赛车中的应用 – 前翼、尾翼的风致振动

 

 

 

 

 

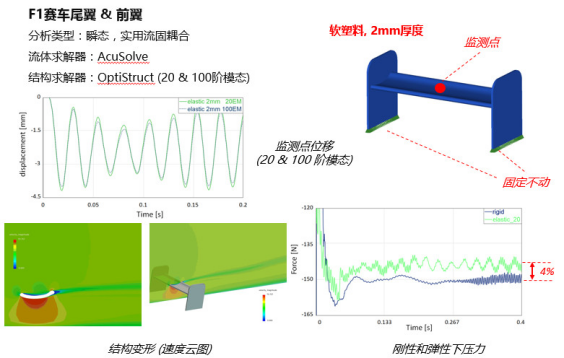
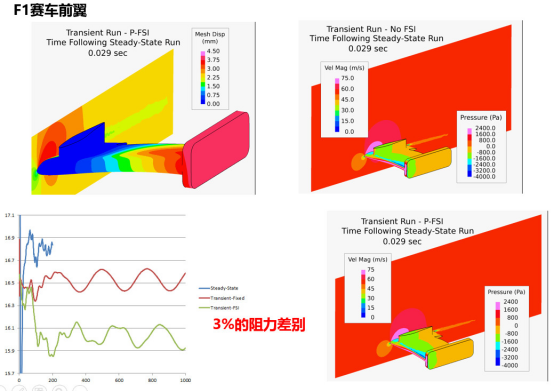
案例3：P-FSI模拟天线的风致振动

 

 

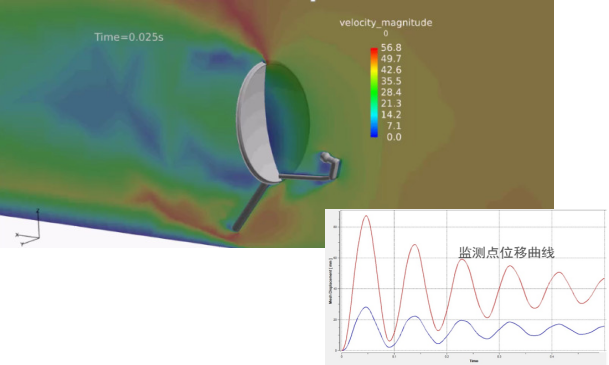
3.2 直接流固耦合

 

直接流固耦合（DC-FSI）是一种需要实时传递数据的双向流固耦合。流体模型和结构模型分别独立建模，流固耦合面的几何必须重叠，但是网格无需一一对应，AcuSolve可自行完成不同网格间的插值。根据使用的结构求解器的不同，在AcuSolve中合理定义外部求解器的参数。两个求解器都会通过预定义的方式分别读取流固耦合面上的流体、结构的计算结果，并实时交互（图5）。

 

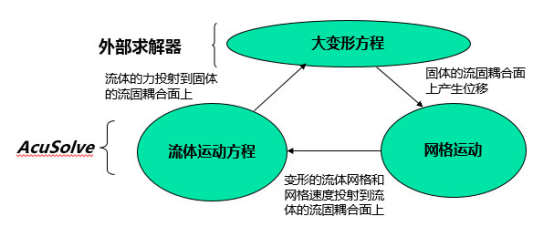
图5. AcuSolve与外部求解器直接耦合的交互迭代

以AcuSolve和RADIOSS为例，两个求解器通过TCP Socket实现通信；可以先启动RADIOSS，也可以先启动AcuSolve，双方都预设了等待时间；AcuSolve和RADIOSS交替迭代时，数据通过流固耦合面（Wetted surface）传递。直接流固耦合的基本计算流程如图6所示：

 

 

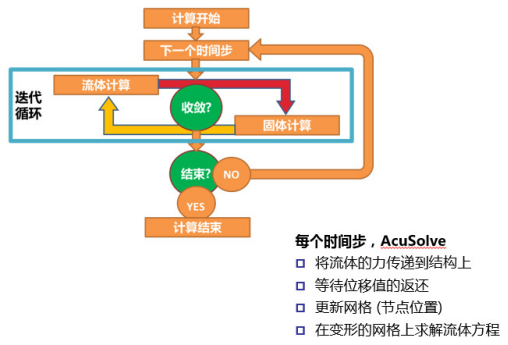
图6. 直接流固耦合的计算流程图

 

直接流固耦合的优势有以下几点：1）不受线性结构变形假设的限制，支持非线性几何和非线性材料，因此适用于线性、非线性结构变形；2）在结构求解器一侧可充分运用结构的建模能力，如多个刚体的连接、梁单元、壳单元和3D单元的混合；3）支持结构应力的直接计算和可视化。

直接流固耦合的局限性体现在：1）建模和计算时间更长，迭代的流程更复杂；2）由于是实时耦合，流体和结构求解的时间步长和总物理时间必须一致；3）结构求解器必须支持非线性计算；4）结构求解器必须支持CCI代码耦合接口。

 

案例1：DC-FSI在风电行业中的应用 – 叶片气弹性

 

 

 

案例2：DC-FSI在海洋工程中的应用 – 涡激振动

 

 

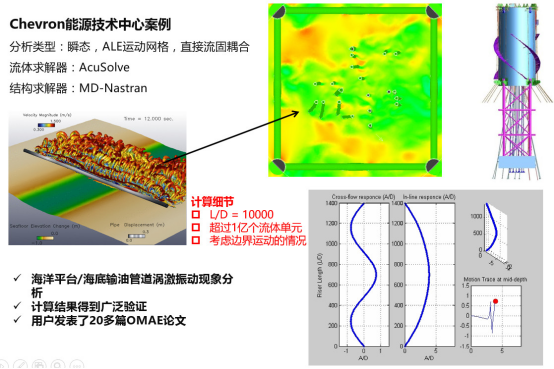
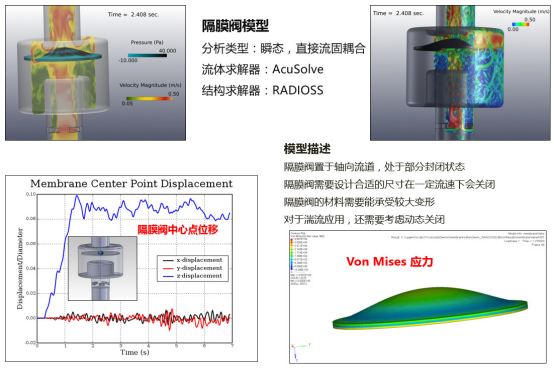
案例3：DC-FSI在流体机械中的应用 – 隔膜阀变形

 

 

4. AcuSolve流固耦合优势总结

AcuSolve的流固耦合功能优势可总结为以下几点：

- 瞬态计算的数值方法鲁棒性极佳；

- 对单元质量的容忍性明显优于其他流体求解器；

- 针对多物理场的计算十分稳健；

- 独创了实用流固耦合（P-FSI）技术；

- 直接流固耦合（DC-FSI）的计算过程中，不需要通过第三方软件实现数据传递；

- 在多个行业积累了众多成功案例。

 

 

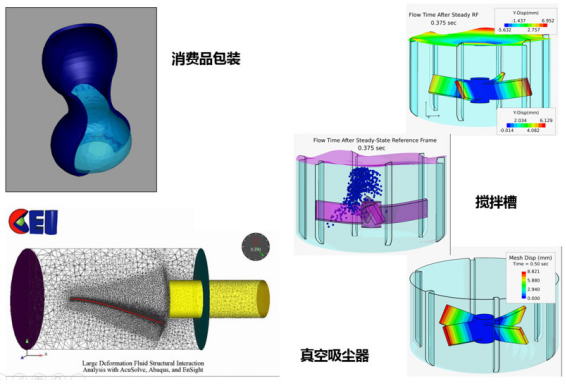
图7. AcuSolve流固耦合案例集锦