一文带你深入理解有限元分析的基础理论

有限元（Finite Element）方法，作为一种高度专业化的工程分析工具，被广泛应用于处理复杂结构中的应力分布、振动特性及热传导等物理难题。其核心思想在于，通过将大型且复杂的结构细分成无数个较小、易于管理的离散单元，再对每个单元独立进行精确的数学建模与计算，最终将这些局部结果综合起来，以全面描绘整个结构在特定条件下的行为与响应。

在这一过程中，结构被巧妙划分为数量有限的单元集合，这些单元可以是适应不同几何形态的一维杆件、二维板壳或三维实体，完全依据被分析对象的特性和需求而定。每个单元内部包含若干节点，它们不仅是单元间相互连接的桥梁，也是传递应力和位移信息的关键点，通过这些节点的相互作用，实现了对整个结构力学行为的精准模拟。

有限元分析基于坚实的数学基础与先进的计算机技术，能够将复杂的物理现象抽象为可解的数学方程，并利用高效的数值算法求解这些方程，从而获取结构在各种工况下的详细力学参数，如应力分布、位移变化及变形形态等。这些信息对于工程师评估结构的强度、刚度、稳定性及耐久性至关重要，为优化设计方案、减少物理试验次数、提升产品质量提供了强有力的支持。

得益于其强大的功能和广泛的应用范围，有限元分析已成为航空航天、汽车制造、土木工程、机械制造等众多工程领域中不可或缺的工具。它不仅极大地促进了工程技术的发展与创新，还有效地降低了研发成本，缩短了产品上市周期，为各行各业带来了显著的经济效益和社会效益。

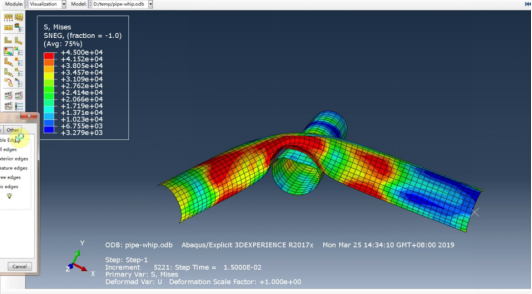
有限元方法的基础理论涉及到数学、物理和工程力学等多个领域，以下是有限元方法的基础理论要点：

1. 离散化：有限元方法首先将连续的结构或物理现象离散化为有限数量的单元，这些单元可以是线性的、二次的或更高阶的。每个单元由节点组成，节点上的位移或其他场量是有限元方法的主要未知数。

2. 变分原理：有限元方法的理论基础是变分原理，即通过对结构的能量或势能进行变分，得到结构的平衡方程。这些平衡方程可以通过变分法推导出来，并且是结构的位移、应力等场量的微分方程。

3. 单元刚度矩阵：每个单元都有其自身的刚度矩阵，描述了单元内部的应力-应变关系。通过对单元的刚度矩阵进行组装，可以得到整个结构的刚度矩阵。

4. 组装：通过组装单元刚度矩阵，可以得到整个结构的刚度矩阵。这需要考虑到单元之间的连接关系和边界条件。

5. 边界条件：在有限元分析中，需要考虑结构的边界条件，这些条件可以是位移固定、载荷施加、约束条件等。

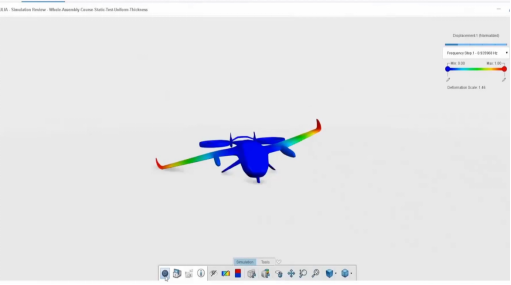
6. 求解：有限元方法通常会使用数值方法来求解结构的平衡方程，如有限差分法、有限元法、边界元法等。

7. 后处理：有限元分析得到的结果需要进行后处理，包括位移、应力、应变、振动模态等信息的提取和分析。

有限元方法的基础理论涉及到多个领域，通过对结构进行离散化，建立变分原理，组装刚度矩阵，考虑边界条件，求解平衡方程和进行后处理，最终得到结构的位移、应力、应变等信息。这些信息可以帮助工程师评估结构的性能和安全性，优化设计方案。