什么是几何非线性分析？谈谈非线性屈曲分析理论

如果物体发生的变形远小于物体自身的几何尺寸，同时材料的应变远小于1，在此条件下，物体的平衡方程可以不考虑物体的位置和形状变化，因此分析中不必区分变形前和变形后的状态，而目在加载和变形过程中的应变可用位移一次项的线性应变进行近似。这类分析称为“小变形分析“，如果不涉及材料非线性及接触非线性，这类分析为线性分析。

实际应用中会遇到很多不符合小变形假设的问题，例如，板和壳等薄壁结构在一定载荷作用下,尽管应变很小，甚至未超过弹性极限，但是位移较大，材料会有较大的位移和转动，这时的平衡方程需要建立在变形后的构形上，以考虑变形对平衡的影响，同时应变表达式也应包括位移的一欢项。这样一来，平衡方程和几何方程都将是非线性方程。这种由于大位移和大转动引起的非线性同题即为几何非线性问题。几何非线性分析涉及的主要问题如下。

1）非线性屈曲分析。

2）跟随力。

本章主要介绍这两个方面的基本理论及0piSuruct中如何进行此类分析，

17.1.1 非线性屈曲基本理论

屈曲是指结构在外部载荷作用下突然发生大的变形，结构失去承载力的力学行为。屈曲分析分为线性屈曲及非线性屈曲。以扁壳为例，如图17-1所示，两端固定的扁壳在顶端受集中力。在线性屈曲分析中，基于小变形假设，通过特征值分析可得到屈曲载荷及屈曲形状，如图17-2所示的A点。在非线性屈曲分析中，当载荷比较小时，分析结果同线性结果一致。当载荷逐步增大、变形逐步增加时，结构响应呈现出非线性，力位秘曲线开始偏离线性结果。如图17-2所示，在B点外载达到最大，之后变形继续变大，但是结构承受的外载变小，结构发生屈曲。以B点到C点，变形维续变大，但是结构承受的载荷继续变小。过了C点以后位移增加，结构承受的载荷开始增加，直至D点达到之前载荷的极限点。从B点到D点的过程称为“疾速跳过（snap through）”。

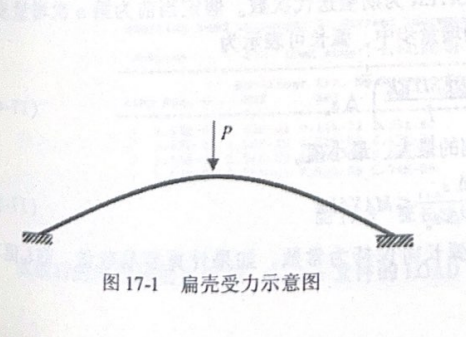
图17-1 扁壳受力示意图

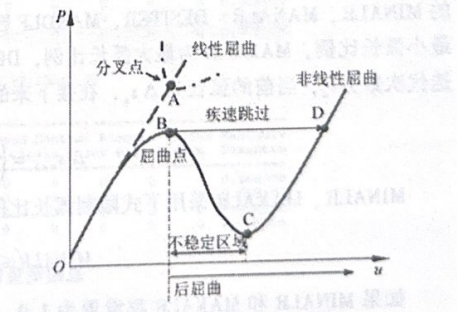
图17-2 扁壳外载作用下的力位移曲线

届曲分析与一般的非线性分析不同的是，力位移曲线不再是凸面，采用传统的牛顿法求解非线性方程时，只能求解 OB段，过了B点牛顿法就会发散。在屈曲分析中，跟踪整个加载路径是非常有意义的，包括BC不稳定区域，因此需要引入新的方程求解方法。弧长法能很好地解决这个问题。在传统的牛顿法中，只有位移是未知数，弧长法与之不同的是，除了位移，载荷大小也是未知数。由于多了一个未知数，故需要添加一个方程。弧长法的基本方程由结构平衡方程及约束方程组成。

平衡方程：R_n+1=F_int+1（u_n+1）-入_n+1P=0

约束方程：f_n+1（u_n+1，入_n+1）=0

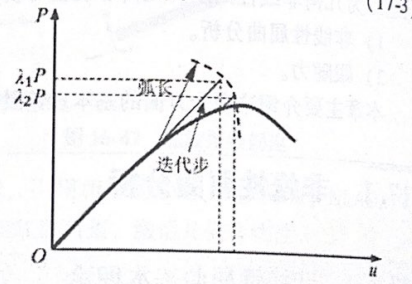
图17-3弧长法迭代求解示意图

式中，n为最后一次收敛的增量步：n+1 为下一个增量步；R_n+1为不平衡力向量；F_int，n+1为内力间量；u_n+1次增量后的位務向量，为未知量；入_n+1为载荷因子，为来知量；P为外力向量。

不同的约束方程构成了不同的孤长法，常用的方法有 Crisfield 方法、RIKS 方法及修正的 RIS方法。下面以 Crisfield 方法为例，简单阐述一下方程求解流程。式中，AS。+1为当前增量步的孤长；4为放缩因子，可通过 NLPCI 卡片上的 SCALE 字段设置。

当4为无穷大时，该方法等效于传统的牛顿法，为载荷控制算法，该方法不能求解后屈曲问题；当¢=0时，为圆柱法，是位移控制算法；当4=1时，为圆球法，表示每个增量步下，载荷增量及位移增量构成的向量模等于该增量步的弧长。圆球法可用图17-3所示方程在一个增量步内选代求解的过程。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。