LAW36的定义

在Altair（Hyperworks）中，LAW36定义几何非线性分析（NLGEOM）中分段线性弹塑性材料的材料属性。需要真实应力-真实塑性应变数据（如下图示例）

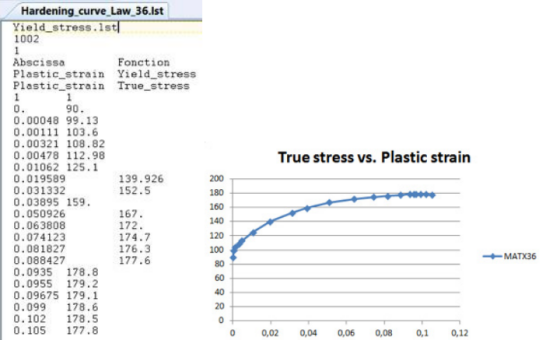
注意：塑性材料应变-应力曲线的第一个点应该是塑性应变为零的点。

要点：曲线必须人为地外推到塑性应变为100%的点。通常只需在真实塑性应变等于100%处添加另一个真实应力数据。这个应力值必须选择稍微超过Rm的值。

这样的推断是必要的，它会告诉求解器对于超过颈缩点的单元如何处理。

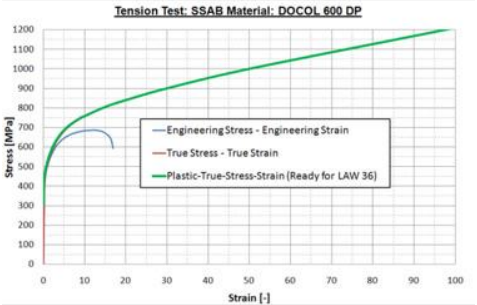
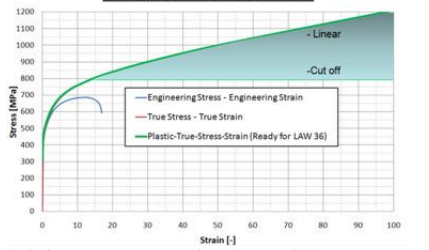
依赖于外推法（例如线性差值或截断），高塑性区单元的应力将连续地增加（线性差值）或者将保持相同的应力值（截断方案）。后者可以被认为一种失效模型，单元会持续变形，但应力等于断裂时的值而不会超过它。

MATX36通过卡片MATX36定义在material collector中（是MAT1的扩展）。

应力-应变曲线定义为TABLES1（卡片是TABLES1的 load collector），通过TPID引用。

LAW2的定义（JOHNSON-COOK；MATX02）

σtr = a + b (εpl)n

上面的方程中，a是屈服应力，Re是弹性极限，b是硬化参数，εpl真实塑性应变，n硬化指数。

与分段线性近似（如LAW36）不同，应力-应变关系根据解析方程在求解器中更快地直接计算得到。

如果真实应力与塑性应变数据是可用，屈服应力（a）直接从曲线中读取。但是b和n应该怎样得到？

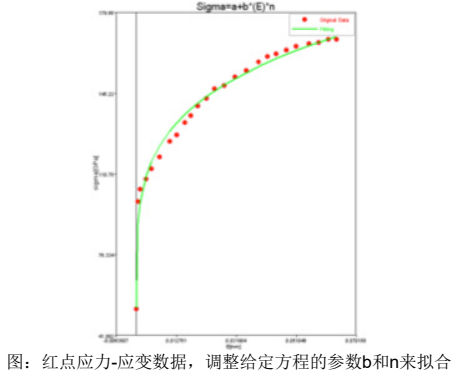
你可以在像HyperMath这样的程序中通过使用曲线拟合确定参数b和n。 下图是利用HyperMath基于应力-应变数据进行拟合，调整参数n和b得到Johnson Cook模型。（运用HyperMath作曲线拟合的例子在教程中有更详细描述）

另外，硬化参数b和指数n可以通过下面的方程确定（a是弹性极限，屈服应力）

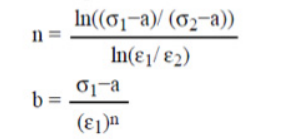
这里点1（σ1和ε1）对应颈缩点的位置，而点2(σ2和ε2)是曲线上的其它点。事实上，推荐对曲线上的每个点计算b和n然后取平均值。因为，b和n的取值严重依赖于点的选择。

对于前面给出的数据（Hardening_curve_law_36.lst），硬化参数b和指数n为：

n = 0.397

b = 229.197 MPa

下图中，显示给定的应力-应变数据（MATX36）和Johnson Cook曲线(基于前面确定的参数)。

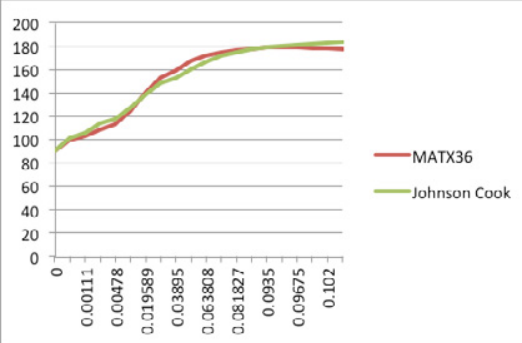
一旦a，b和n已知，就可以在包含MAT1及扩展卡片MATX02的material collector中定义Johnson Cook材料。