线性屈曲分析：弹性屈曲_Altair帮助文档

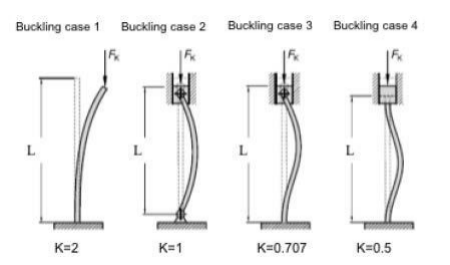
图: 欧拉屈曲案例; K=有效屈曲长度因子; L=柱的长度

(来自Läpele, Volker: Einführung in die Festigkeitslehre; Vieweg+Teubner Verlag; 2011)

 

1757年，Leonhard Euler 推导出以下方程：

Fcrit = π2 Ε Ι / (K L)2 = π2 Ε Ι / s2

在此

F = 最大或临界力（柱向的垂直力）

E = 弹性模量

I = 面积惯性矩（第二面积矩）

L = 柱长

K = 柱有效长度因子，其值取决于柱端的支撑状态，如下：

两端铰接（自由旋转），K = 1.0

两端固定，K = 0.50

一端固定，一端铰接，K = 0.707

一端固定，一端自由，K = 2.0

 KL = 柱的有效屈曲长度

换句话说，临界力取决于：

 

• 柱长

• 横截面（第二表面积矩）

• 材料属性（杨氏模量，若为弹性材料）

• 边界条件（边界条件决定弯曲模态和变形的圆柱上各拐点的距离，拐点的距离越近，圆柱导致的结果越高）

 

圆柱的强度因材料分配而增加以提高惯性矩。可通过将材料尽可能分布到远离中心轴的横截面而不增加圆柱的重量来实现，同时保持材料厚度而不发生局部屈曲。这就验证了一个众所周知的事实，对于柱体来讲，一个管截面会比一个实心结构效果更好。

 

注：真实的建筑常常存在一些缺陷，比如，预变形，载荷尚未达到理想临界值而发生大变形或失效。线性屈曲分析常常高估了结构的强度与稳定性，从而导致非保守结果。因此，它不应作为唯一的衡量标准。然而，线性屈曲分析至少提供了预期的变形形状信息。

 

看看欧拉方程，并除以面积A定义屈曲发生的临界应力：

σkrit = Fcrit / A ≤ Re

 其中Re为弹性极限：

σkrit = Fcrit / A = π2 E I / A s2 = π2 E / λ2 ≤ Re

 且

λ = s / √ (I / A)

 

图: 欧拉屈曲案例; K=有效屈曲长度因子; L=柱的长度

(来自Läpele, Volker: Einführung in die Festigkeitslehre; Vieweg+Teubner Verlag; 2011)

 

1757年，Leonhard Euler 推导出以下方程：

Fcrit = π2 Ε Ι / (K L)2 = π2 Ε Ι / s2

在此

F = 最大或临界力（柱向的垂直力）

E = 弹性模量

I = 面积惯性矩（第二面积矩）

L = 柱长

K = 柱有效长度因子，其值取决于柱端的支撑状态，如下：

两端铰接（自由旋转），K = 1.0

两端固定，K = 0.50

一端固定，一端铰接，K = 0.707

一端固定，一端自由，K = 2.0

 KL = 柱的有效屈曲长度

换句话说，临界力取决于：

 

• 柱长

• 横截面（第二表面积矩）

• 材料属性（杨氏模量，若为弹性材料）

• 边界条件（边界条件决定弯曲模态和变形的圆柱上各拐点的距离，拐点的距离越近，圆柱导致的结果越高）

 

圆柱的强度因材料分配而增加以提高惯性矩。可通过将材料尽可能分布到远离中心轴的横截面而不增加圆柱的重量来实现，同时保持材料厚度而不发生局部屈曲。这就验证了一个众所周知的事实，对于柱体来讲，一个管截面会比一个实心结构效果更好。

 

注：真实的建筑常常存在一些缺陷，比如，预变形，载荷尚未达到理想临界值而发生大变形或失效。线性屈曲分析常常高估了结构的强度与稳定性，从而导致非保守结果。因此，它不应作为唯一的衡量标准。然而，线性屈曲分析至少提供了预期的变形形状信息。

 

看看欧拉方程，并除以面积A定义屈曲发生的临界应力：

σkrit = Fcrit / A ≤ Re

 其中Re为弹性极限：

σkrit = Fcrit / A = π2 E I / A s2 = π2 E / λ2 ≤ Re

 且

λ = s / √ (I / A)