RADIOSS线性稳定性分析_CAE教程

在有限元分析中的线性屈曲分析，首先通过对结构施加一个参考水平的载荷线性Fref来解决。施加的是一个理想的单位载荷F。单位载荷和相应的约束，SPC，在第一个载荷步、工况下引用。 接下来执行一个标准的线性静态分析来获取用以生成几何刚度矩阵KG的应力。接着，其屈曲载荷会做为第二个载荷步、工况的一部分通过求解特征值问题计算出来。

(K-λKG)x=0

K是结构的刚度矩阵，λ是参考载荷的乘数。特征值问题的求解通常成生n个λ（屈曲载荷因子），其中n是自由度的数目（实际上，仅会计算出特征值的一个子集）。向量x是与特征值对应的特征向量。

特征值问题通过一个称之为“Lanczos法”的矩阵法来求解。并非所有的特征值都是必需的，对于屈曲分析只需要计算最小特征值的一小部分。最小特征值与屈曲有关，临界或屈曲载荷为：

Fcrit = λcrit Fref

 换句话说,

λcrit = Fcrit / Fref

 因此

λc < 1 buckling

λc > 1 safe

 注：屈曲分析中所得到的位移结果可将屈曲模态的振型描述出来。

任何位移结果都是无意义的，同样适用于屈曲分析中的应力应变结果。

从理论到实践: 怎么样去设置屈曲分析

为了运行线性屈曲分析，需要以下两步：

第一步：

三个载荷集与两个载荷步、工况必须定义：

• 约束的载荷集 (SPC =单点约束; 不需要Card Image)

• 载荷的载荷集 (理想的单位载荷)；不需要Card Image

• 另一个载荷集(需要Card Image EIGRL)定义屈曲模态的数量(card image 如下)

• ND = 1: 使RADIOSS提取出第一阶屈曲模态

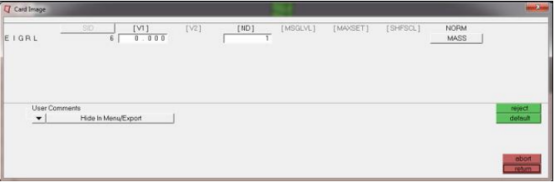
第二步

定义两个工况：一个静态和一个屈曲。载荷集SPCs和单位载荷定义一个静态工况。注意此工况的type设为linear static：

接下来定义屈曲工况（需要静态工况的结果）：

如前，SPC引用模型约束，STATSUB (BUCKLING)引用之前的静态工况，最后，METHOD引用提取屈曲模态根数目信息的载荷集（例如EIGRL）。同时要注意，此时type要设为linear buckling。

注：

• STATSUB不可调用带有惯性释放的工况。

• 屈曲分析将忽略0维单元、MPC、RBE3和CBUSH单元等。

• 这些单元可用于屈曲分析，但对几何刚度矩阵KG无作用。

• 默认情况下，不包括刚性单元对几何刚度矩阵的贡献。用户必须在bulk data片段中添加PARAM、KGRGD、YES使之包括刚性单元对几何刚度矩阵的贡献。

• 另外，用户可通过EXCLUDE工况信息条目，决定忽略其他单元对几何刚度矩阵的贡献，使用户有效的去控制结构的哪些部分可用于屈曲分析。这此去除掉的属性仅仅是从几何刚度矩阵中移除，从而使屈曲分析处于弹性边界状况。这就意味着这些去除的属性依然会在屈曲模态中显示其运动。